Question

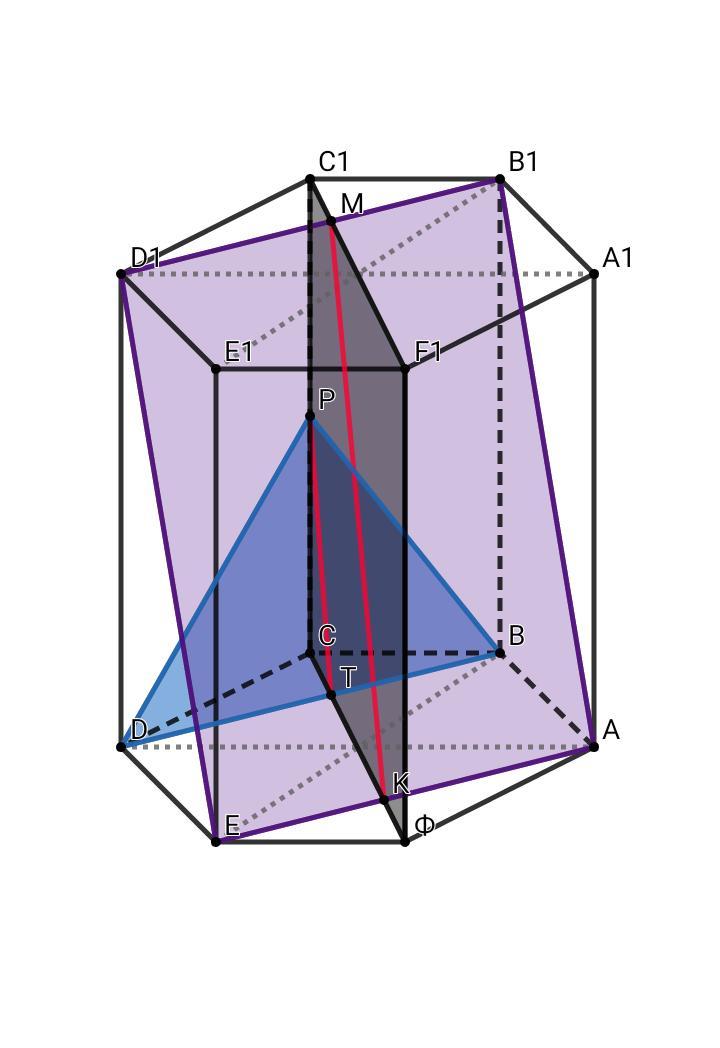
Дана правильная шестиугольная призма ABCDEFA₁B₁C₁D₁E₁F₁. Точка P - середина бокового ребра CC₁.

Найдите расстояние между прямыми BP и AB₁ , если сторона основания призмы равна 6, а боковое ребро равно 2√3

Answer 1

Плоскости BPD и АВ1D1, в которых лежат прямые BP и АВ1, параллельны по признаку параллельности двух плоскостей (АЕ || BD, PT || AB1). Проведём перпендикулярную плоскость CFF1, которая пересекает эти плоскости по прямым ТР и МК.

Расстояние между паралельными прямыми РТ и МК равно искомому расстоянию между прямыми ВР и АВ1.

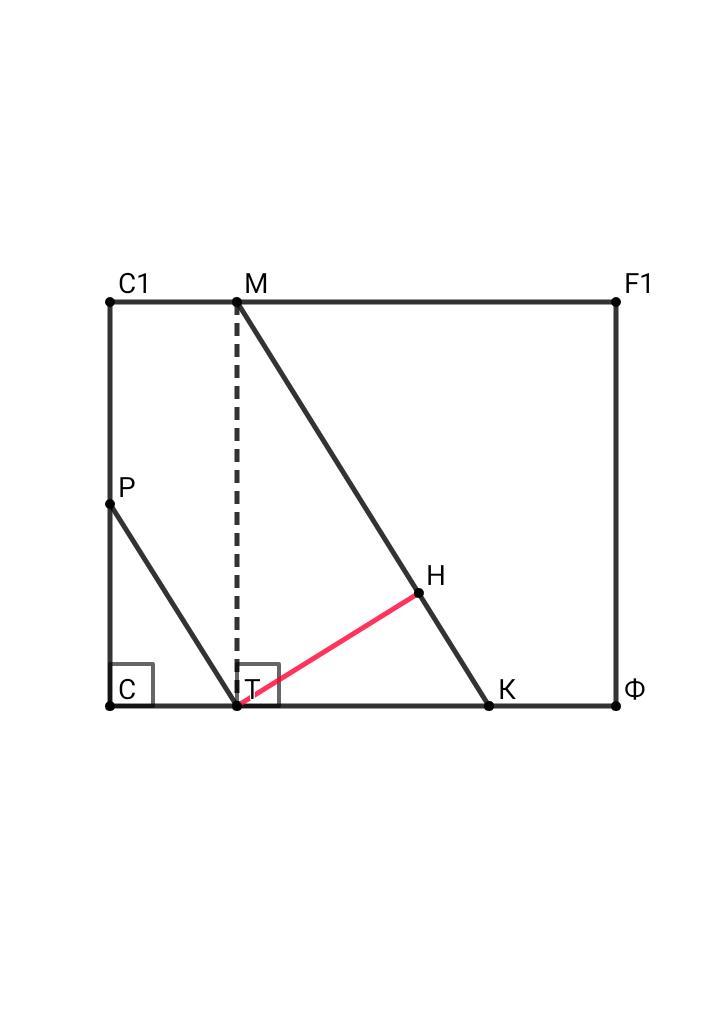
Рассмотрим прямоугольник СС1F1F:  CF = 2•AB = 2•6 = 12

CT = KF = CF/4 = 12/4 = 3 , TK = 6

В прям.ΔMTK: по т.Пифагора:

МК² = МТ² + ТК² = (2√3)² + 6² = 12 + 36 = 48

МК = 4√3

Площадь ΔТМК: S = MT•TK/2 = MK•TH/2

MT•TK = MK•TH ⇒ TH = MT•TK/MK = 2√3•6/4√3 = 3

Следует отметить, что тангенс угла наклона данных плоскостей равен √3/3, то есть угол наклона равен 30°

ОТВЕТ: 3