Question

Задача по геометрии:
В правильной треугольной пирамиде сторона основания равна корню 3, а высота пирамиды равна 4
найдите:
а)тангенс двугранного угла при основании пирамиды
б)площадь полной поверхности пирамиды

Answer 1

Дано: треуг. АВС - равностор., АВ=

$\sqrt{3}$

, SO=4.

Найти: a). tg угла SFO

b). Sполн.

Решение:

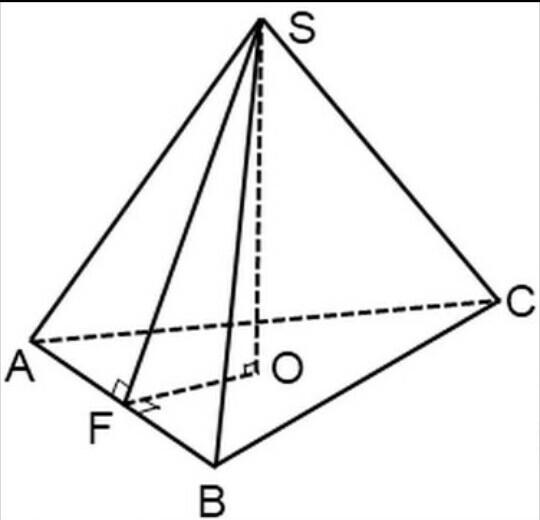
a). Рассмотрим треуг. SFO: угол О=90 град(т.к. SO-высота), FO=r(по определению, в правильной треугольной пирамиде высота проецируется в центр вписанной окружности => FO=r).

r=S÷p (где S-площать треуг. АВС, р-полупериметр треуг. АВС).

$s = \frac{ {a}^{2} \sqrt{3} }{4} = \frac{3 \sqrt{3} }{4}$

$p = \frac{ \sqrt{3} + \sqrt{3} + \sqrt{3} }{2} = \frac{ 3 \sqrt{3} }{2}$

$r = \frac{3 \sqrt{3} }{4} \div \frac{3 \sqrt{3} }{2} = \frac{3 \sqrt{3} \times 2 }{3 \sqrt{3} \times 4 } = \frac{1}{2}$

Получается, FO=0,5; SO=4.

tg угла SFO=SO/FO=4/0,5=8.

b). Sполн=Sосн+3Sбок

Из треуг. SFO найдем SF:

$\sqrt{ {4}^{2} + {0.5}^{2} } = \sqrt{16 + 0.25} = \sqrt{ \frac{65}{4} }$

Sбок=АВ×SF×1/2=

$\frac{1}{2} \times \sqrt{3} \times \sqrt{ \frac{65}{4} } = \frac{1}{2} \times \sqrt{ \frac{195}{4} } = \frac{1}{2} \times \frac{ \sqrt{195} }{2} = \frac{ \sqrt{195} }{4}$

Sполн=

$\frac{3 \sqrt{3} }{4} + \frac{3 \sqrt{195} }{4} = \frac{3 \sqrt{3} + 3 \sqrt{195} }{4}$

Ответ: а). 8.

б).

$\frac{3 \sqrt{3} + 3 \sqrt{195} }{4}$