Предмет: Алгебра,
автор: brakoff2003
Найти сумму нескончаемой геометрической прогрессии -4*sqrt(2); 4; -2*sqrt(2);
Приложения:
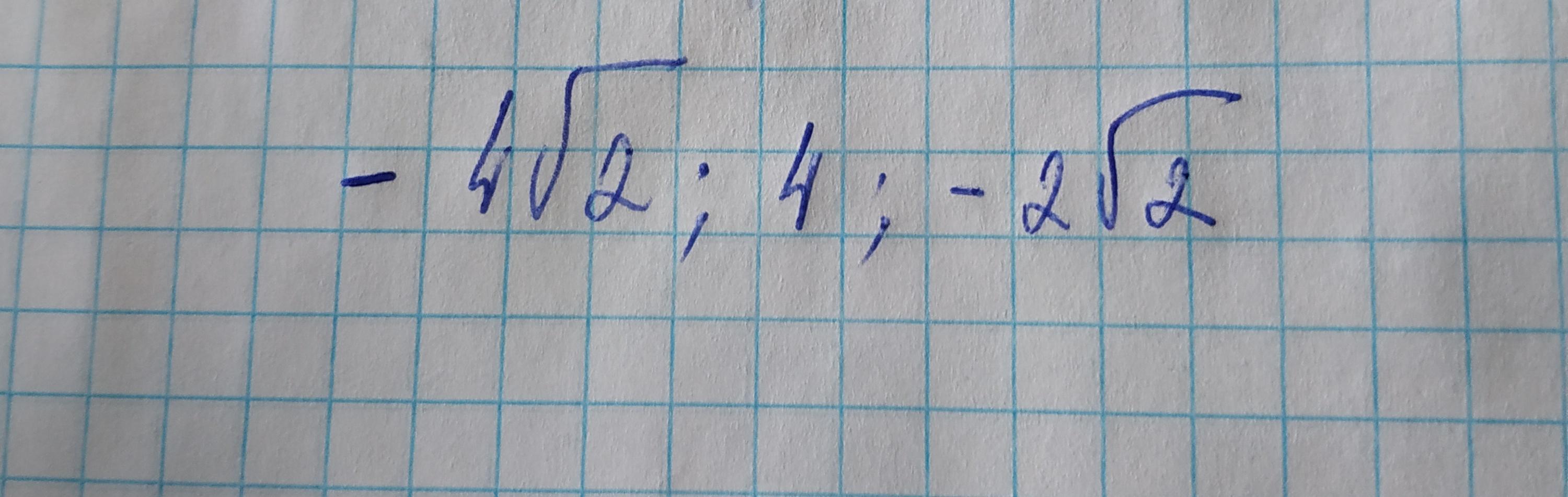
Ответы
Автор ответа:
1
Ответ:
S=-4(2-√2)
Объяснение:
Dano:-4V2,4,-2V2
Obliczamy d d=4/-4V2=-V2/2 (-1<q<1)
* пользуемся формулой: S=a1/(1-q), который настоящий, если: -1< q<1
a1=-4√2
q=-√2/2
S=a1/(1-q)
S=-4√2/(1-(-√2/2)) = -4√2/(2+√2)/2) =-4√2*2/(2+√2)= -8√2/(2+√2)= =[-8√2*(2-√2)]/[(2+√2)(2-√2)=
=(-16+8√2)/(4-2)=-8(2-√2) /2=-4(2-√2)
S=-4(2-√2)
Похожие вопросы
Предмет: Химия,
автор: pashamarkov10556
Предмет: Математика,
автор: ekaterina875113790
Предмет: История,
автор: saliihaa
Предмет: Физика,
автор: smirnykh2012