Предмет: Геометрия,
автор: vitalina4543
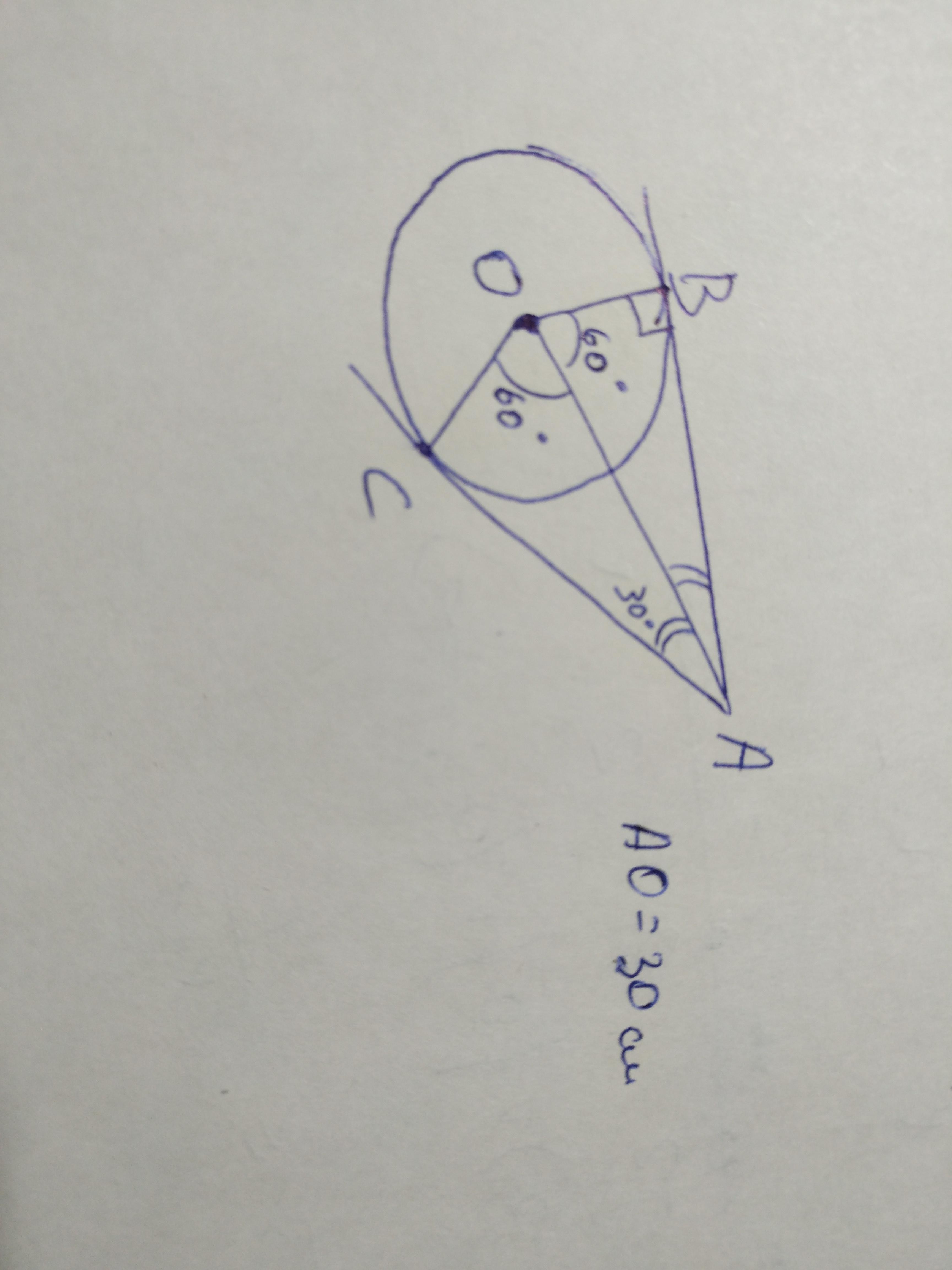
Прямые АВ и АС касаются окружности с центром О в точках В и С. Найдите радиус окружности, если ∠ВОС = 120º, АО = 30 см.
Ответы
Автор ответа:
0
Ответ:
Объяснение:
Катет, лежащий в прямоугольном треугольнике против угла в 30 градусов, равен половине гипотенузы.
Ответ: 15 см
Приложения:
Автор ответа:
0
Т.к. точки В и С - точки касания к окружности, проведенных касательных из точки А, то ОВ⊥АВ, ОС⊥АС, точка О равноудалена от сторон угла ВАС, т.е. лежит на биссектрисе и делит угол ВОС пополам, по 60°, но тогда в треугольнике ВОА угол ВАО =30°, и против него лежит радиус ОВ, т.к. он лежит против угла в 30°, то равен половине гипотенузы АО, ОВ=АО/2=30/2=15/см/
Похожие вопросы
Предмет: Алгебра,
автор: timurturgaliev9
Предмет: Информатика,
автор: Annella54
Предмет: Английский язык,
автор: kaliyeva0421
Предмет: Литература,
автор: AnnaAnna20056
Предмет: Геометрия,
автор: eGoRyan12