Предмет: Алгебра,
автор: iliahook893
Решите ПЖПЖПЖПЖПЖПЖПЖПЖПЖ
Приложения:
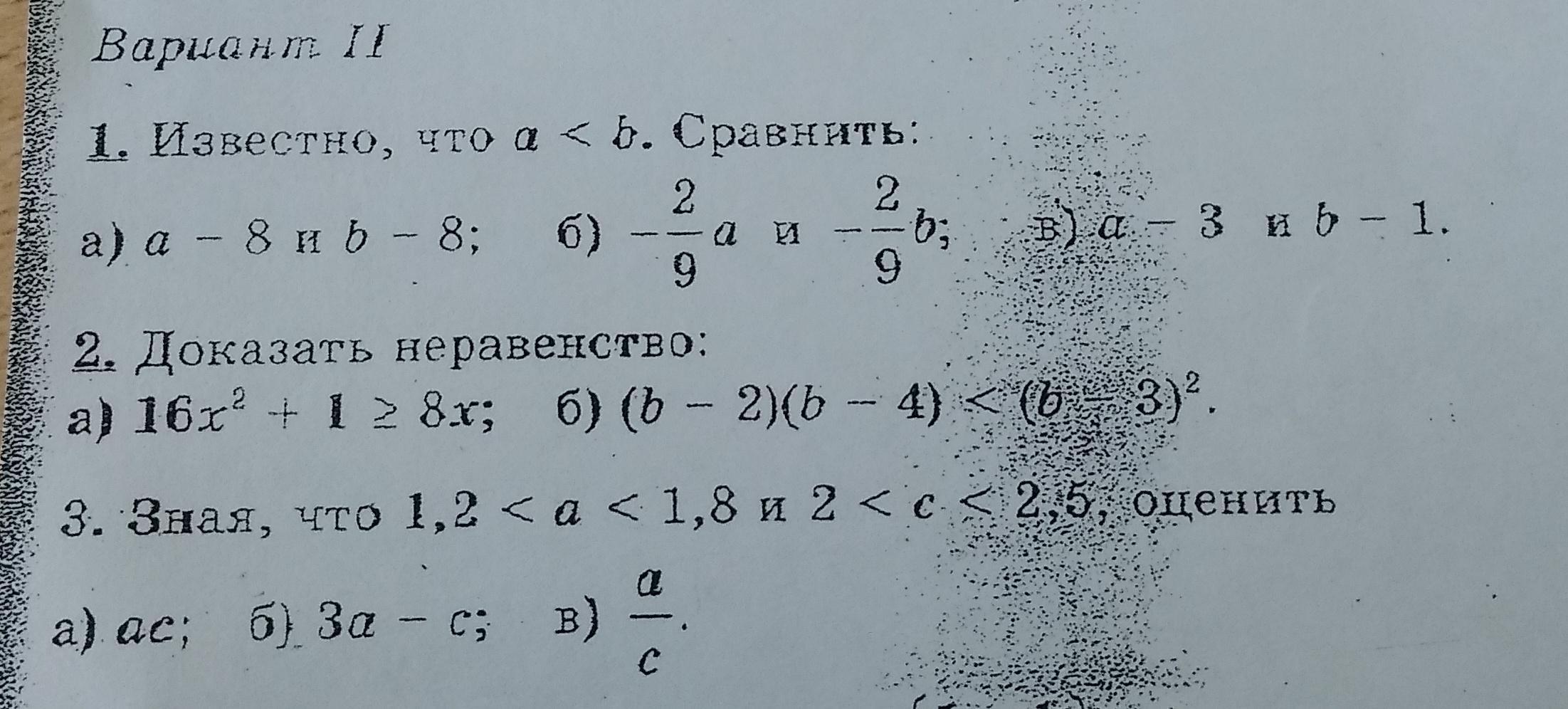
Ответы
Автор ответа:
1
2.
так как дискриминант равен нулю, то график функции кончается Оси ОХ только в одной точке. ветви направлены вверх, так как коэффициент при х^2 >0. следовательно область значений от 0 до бесконечности. следовательно, утверждение выше верное.
3
Похожие вопросы
Предмет: Геометрия,
автор: evatkachuk07
Предмет: Английский язык,
автор: adilet2249
Предмет: Информатика,
автор: cyberpure
Предмет: Математика,
автор: Crasys
Предмет: Информатика,
автор: депутатша