Предмет: Алгебра,
автор: rudenkomiha
Как решить пример по математике?
Приложения:
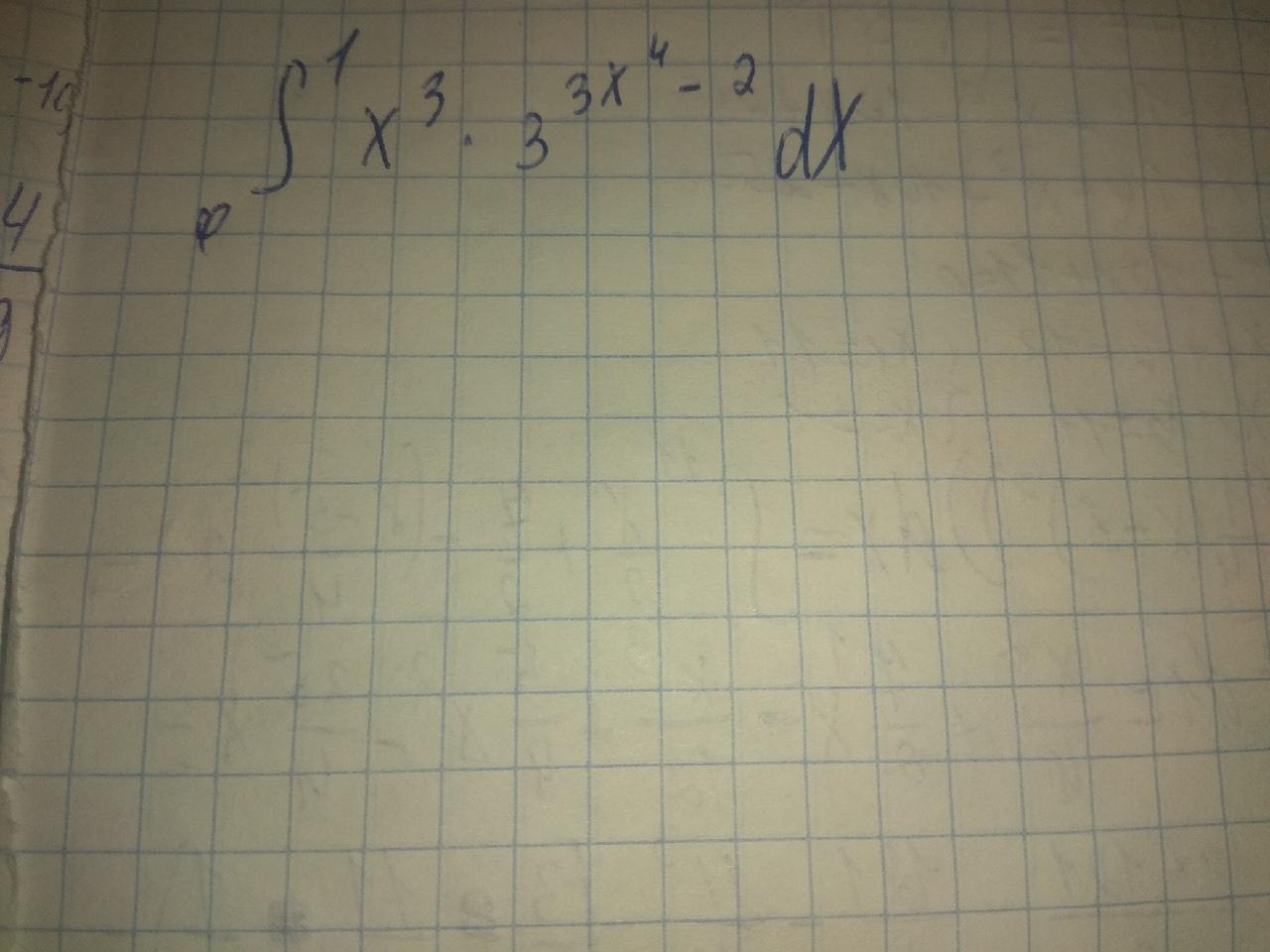
rudenkomiha:
Дам 100 баллов
что внизу написано?
Ответы
Автор ответа:
0
Похожие вопросы
Предмет: Биология,
автор: tortik123453
Предмет: Окружающий мир,
автор: avaliullova0
Предмет: География,
автор: timkabimka44
Предмет: Математика,
автор: Аноним
Предмет: Математика,
автор: PerryLeet