Предмет: Математика,
автор: trieskinas
5 задание
sin2x+sin3x=0
полное решение
Приложения:
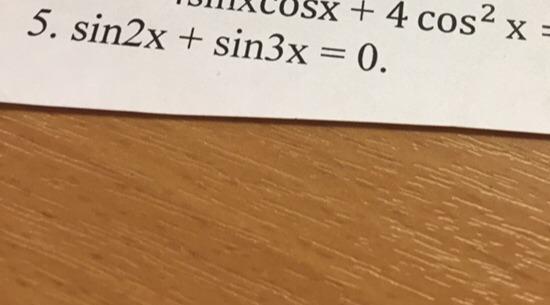
Ответы
Автор ответа:
0
Воспользуемся формулой сумма синусов.
Второе множество не пересекается с первым, т.к. период разный, но место решения второго множества на тригонометрическом круге, полностью совпадает с местом решения первого множества. Т.к. при n={0,5,10...} получается выражение кратное 2πn.
Ответ:
Похожие вопросы
Предмет: Алгебра,
автор: juventus2008nikita
Предмет: Другие предметы,
автор: aboba5456
Предмет: Литература,
автор: vikakohman2
Предмет: Обществознание,
автор: Nikita25199
Предмет: История,
автор: megamozgwins