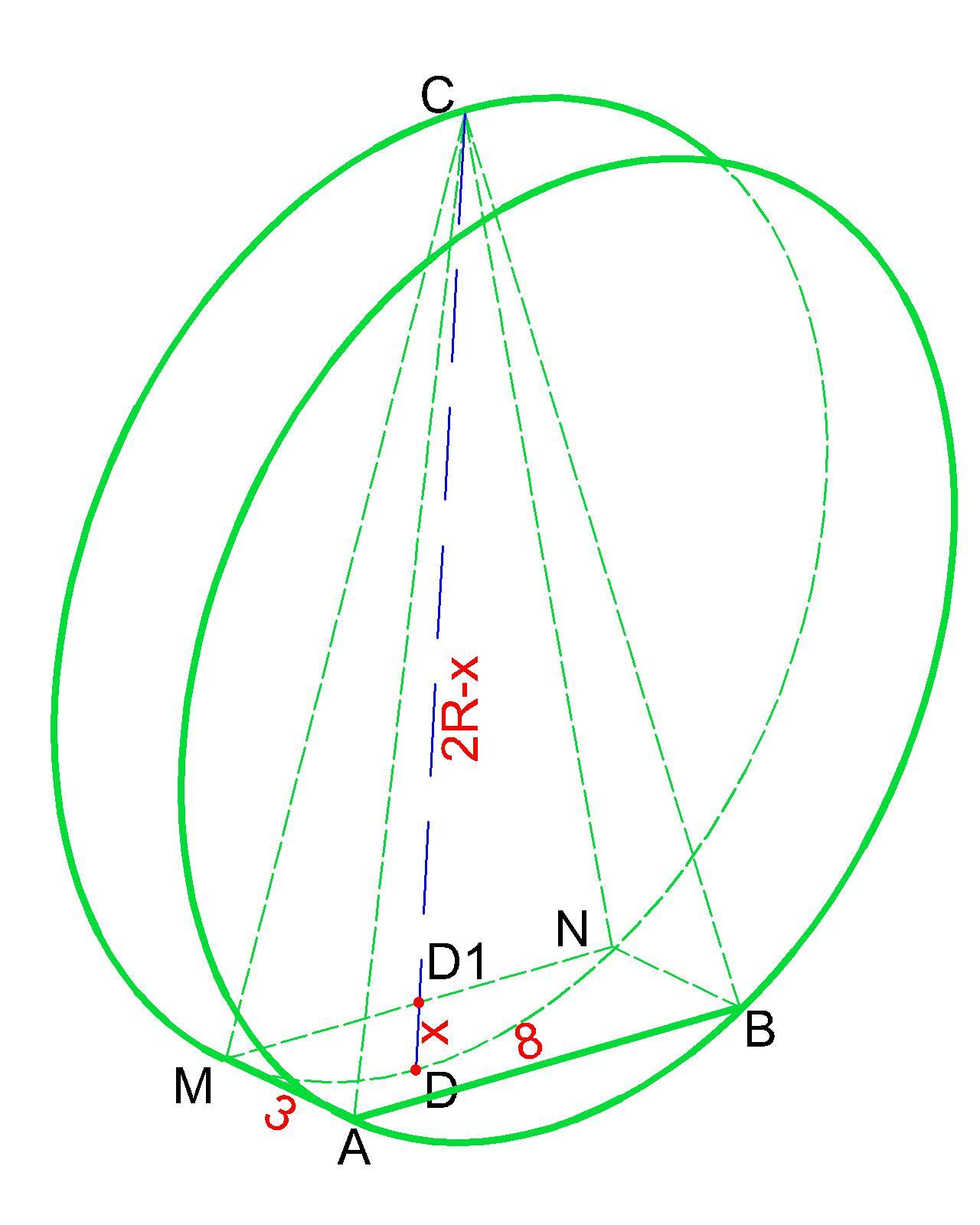
Дан прямой круговой цилиндр высотой 3 и радиусом 8. В одном из основании проведена хорда AB равная радиусу основания, а в другом основании проведен диаметр CD перпендикулярный прямой AB.
Построено сечение цилиндра плоскостью ABNM, перпендикулярной прямой CD, причём Точка C и центр основания цилиндра, содержащего отрезок CD, лежат по одну сторону от плоскости сечения
А) докажите, что диагонали четырехугольника ABNM равны
Б) Найдите объем пирамиды CABNM.
Очень срочно, помогите пожалуйста! 11 класс..
Ответы
Ответ:
Объяснение:
А) докажем что АВNM - прямоугольник.
Имеем 2 параллельные плоскости - основания цилиндра. Плоскость, проходящая через хорду АВ перпендикулярна прямой CD, лежащей в плоскости основания. Значит плоскость сечения перпендикулярна плоскостям основаниий цилиндра, а т.к. цилиндр прямой, то и высоты цилиндра AM и BN, образованные сечением ABNM перепендикулярны плоскостям оснований. В результате получаем четырёхугольное сечение, все внутренние углы которого прямые. Это - прямоугольник.
Диагонали прямоугольника равны!
Б) Найдём объём пирамиды CABNM.
Формула вычисления объёма пирамиды
V=1/3·S·h, где S-площадь основания, h-высота пирамиды.
Очевидно, что S=8*3=24.
Найдём h=CD₁.
Используем свойство хорд: если 2 хорды окружности пересекаются, то произведение отрезков одной хорды равно произведению отрезков другой хорды.
В нашем случае хордами выступают MN=AB=R и CD=2R.
Хорда MN делится на MD₁=ND₁, т.к. хорда CD является диаметром и пересекает хорду MN под прямым углом, разделяя её пополам.
Составим уравнение, обозначив за х D₁D - меньшую часть хорды CD отсеченную плоскостью ABNM:
x·(2R-x) =0.25R²
Для удобства дальнейших расчетов подствим вместо R числовое значение:
х·(16-х)=16
х²-16х+16=0
D=16²-4*16=192
x₁=(16+√192)/2=8+4√3
x₂=(16-√192)/2=8-4√3
Здесь решение x₁ - это случай, когда точка D и центр основания лежат по одну сторону от плоскости сечения (т.к. в нашем случае там находится точка С, то это и есть высота пирамиды,
а х₂ - это отрезок DD₁ изначально принятый за х.
Значит DD₁=8-4√3 и проверим высоту пирамиды
h=CD₁=(2R-x)=16-8+4√3=8+4√3 (совпало с х₁) - это можно выпустить. Простая проверка.
V=1/3·S·h=1/3·24·(8+4√3)=64+32√3 кубических единиц.