Question

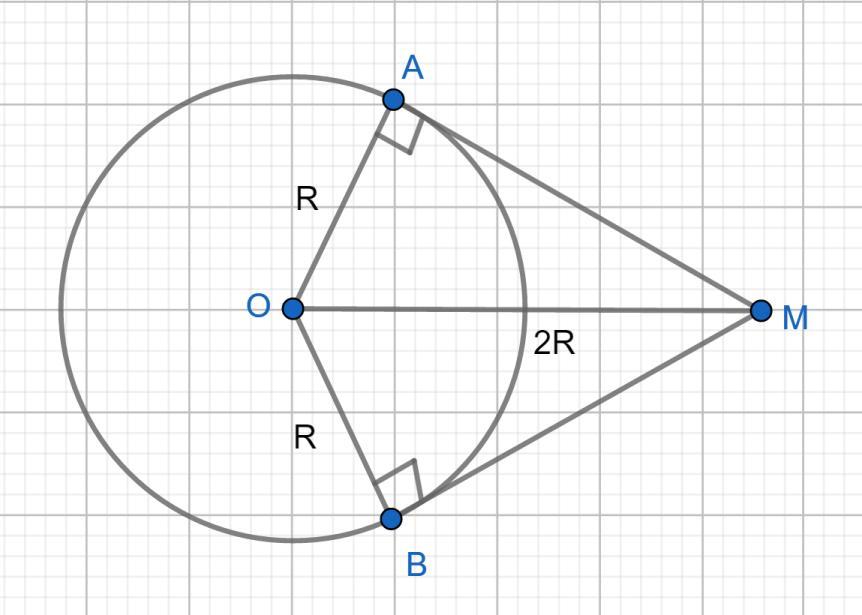
Две прямые касаются окружности с центром О в точках А и В и пересекаются в точке М. Найдите угол между этими прямыми, если ОМ=2R?
Срочнооооооо!

Answer 1

ΔAOM = ΔBOM по 3 признаку - по трем сторонам, AO=OB радиусы, OM общая, AM=BM отрезки касательных, проведенных из одной точки. ⇒ OM биссектриса угла AMB.

∠A= 90° (угол между касательной и радиусом).

В ΔAOM sin∠AMO = AO/MO = R/2R = 1/2 ⇒∠AMO = 30°, ∠AMB = 2*30° = 60°

Угол между касательными 60°.