Предмет: Геометрия,
автор: Polinka0898
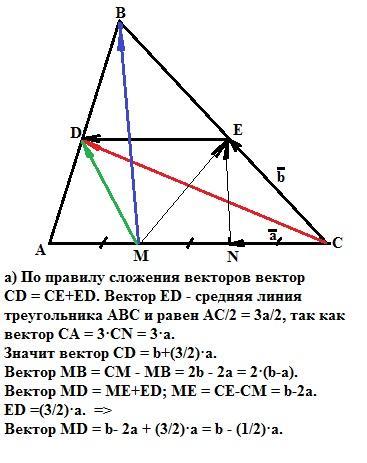
Точки D и E - середины сторон AB и BC треугольника ABC, а точки M и N лежат на стороне AC, причем AM=MN=NC,вектор CN = a,вектор CE = b.
а) Выразить векторы CD,MB.MD через векторы а и b.
б) Докажите с помощью векторов, что MB параллелен NE.
Ответы
Автор ответа:
0
Ответ:
а) CD= b+(3/2)·a. MB= 2·(b-a). MD= b- (1/2)·a.
б) доказательство в объяснении.
Объяснение:
a) По правилу сложения векторов вектор CD = CE+ED. Вектор ED - средняя линия треугольника АВС и равен АС/2 = 3а/2, так как вектор СА = 3·СN = 3·a. Значит вектор CD = b+(3/2)·a.
Вектор МВ = СМ - MB = 2b - 2a = 2·(b-a).
Вектор MD = ME+ED; ME = CE-CM = b-2a. ED =(3/2)·a. =>
Вектор MD = b- 2a + (3/2)·a = b - (1/2)·a.
б) Вектор NE = b-a. Вектор МВ = 2·(b-a). Следовательно, вектор NE СОНАПРАВЛЕН вектору МВ, то есть, параллелен ему, что и требовалось доказать.
Приложения:
Похожие вопросы
Предмет: Математика,
автор: sryvkov08
Предмет: История,
автор: timuruteev1337
Предмет: Химия,
автор: kirilld667
Предмет: Алгебра,
автор: cyxarik
Предмет: Алгебра,
автор: kseniyashushura