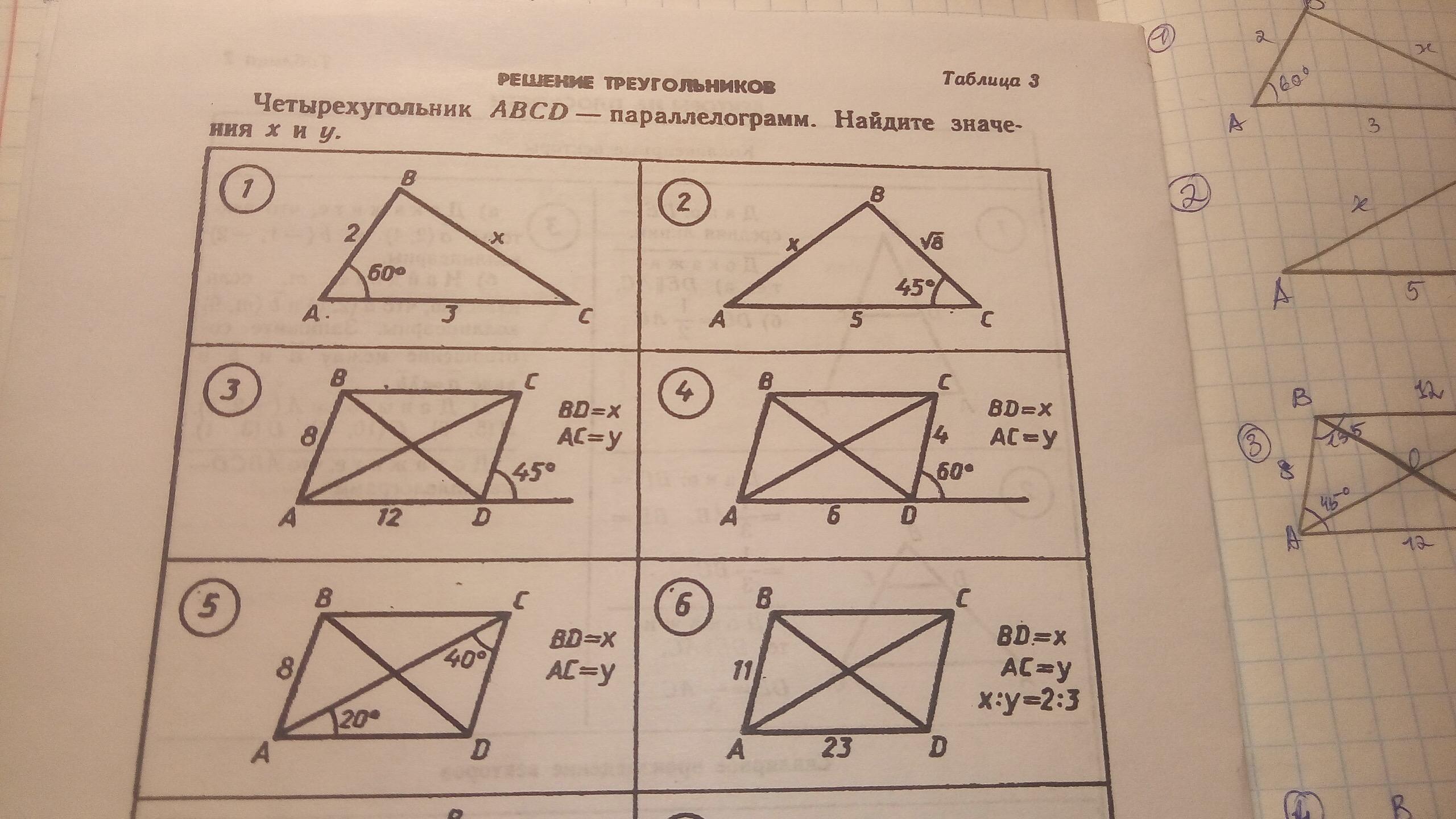
Помогите решить 3 задачу и 5 и 6 тоже
Ответы
Ответ:
3. АС ≈ 18,5 ед. BD ≈ 8,5 ед.
5. АС = 20 ед. BD = 9 ед.
6. АС = ≈ 29,7 ед. BD ≈ 20,5 ед.
Объяснение:
3. ABCD - параллелограмм, значит <A=<45°, как соответственные при параллельных АВ и CD и секущей AD. По теореме косинусов для треугольника АВD:
BD² = AB²+AD² - 2*AB*AD*Cos45 или
BD² = 64+144 - 2*8*12*√2/2 = 208 - 96√2 ≈ 72,2. => BD ≈ 8,5 ед.
Так как <B = 180 - <A, то CosB = - CosA = -√2/2 и тогда в треугольнике АВС:
AC² = 64+144 + 2*8*12*√2/2 = 208 + 96√2 ≈ 343,8. => АС ≈ 18,5 ед.
Ответ: BD ≈ 8,5 ед. АС ≈ 18,5 ед.
5. В параллелограмме ABCD AB =CD. <ADC = 180-40-20 = 120° (из суммы углов треугольника АCD). Вспомним, что Sin120° = Sin(180-60) = Sin60°.
В треугольнике ACD по теореме синусов:
AC/Sin120 = 8/Sin20 => AC = 8*√3/2*Sin20 ≈ 4*√3/0,342 ≈ 20 ед.
AD/Sin40 = 8/Sin20 => AD = 8*Sin40/Sin20 ≈ 8*0,643/0,342 ≈ 15 ед.
По теореме косинусов:
BD² = 64+225 - 2*8*15*√3/2 = 289 -120√3 ≈ 81. => BD =9 ед.
Ответ: АС = 20ед. BD = 9 ед.
6. BD² = 121 + 529 - 2*11*23*Cosα = 650 - 506*Cosα
AC² = 121 + 529 + 2*11*23*Cosα = 650 +506*Cosα
BD²/AC² = (650 - 506*Cosα)/(650 +506*Cosα) = 4/9 => Cosα ≈ 0,454.
Тогда BD = √(650 - 506*0,454) ≈ √420,3 ≈ 20,5 ед.
Соответственно АС = √(650 + 506*0,454) ≈ √879,7 ≈ 29,7 ед.
Ответ: АС = ≈ 29,7 ед. BD ≈ 20,5 ед.