Предмет: Геометрия,
автор: Fufkaa
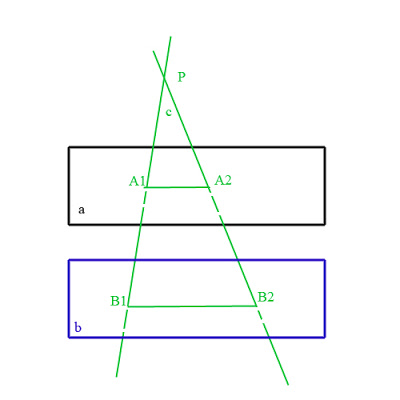
Даны две параллельные плоскости и лежащая между ними точка P.Две прямые,
проходящие через точку Р, пересекают ближнюю к точке Р плоскость в
точках А1 и А2, а дальнюю в точках В1 и В2 соответственно.Найдите длину
отрезка В1В2, если А1А2= 10 см. и РА1:А1В1=2:3
Ответы
Автор ответа:
0
Решение:Плоскости a и b параллельны (по условию)
Проведем плоскость через 3 точки P, B1, B2 (назовем ее плоскость с)- эта плоскость пересекает две параллельные плоскости.
Плоскость с пересекает плоскость a по прямой A1A2.
Плоскость с пересекает плоскость b по прямой B1B2.
Так как a||b, то и A1A2||B1B2.
Отсюда следует что треугольники PA1A2 и PB1B2 подобны (по трем углам (угол Р - общий, а углы PA1A2 и PB1B2, PA2A1 и PB2B1 равны как соответствующие углы при параллельных прямых))
РА1 : PВ1 = 2:5
РА1 : PВ1=A1A2 : B1B2
2:5=10:B1B2
2B1B2=50
B1B2=25
Проведем плоскость через 3 точки P, B1, B2 (назовем ее плоскость с)- эта плоскость пересекает две параллельные плоскости.
Плоскость с пересекает плоскость a по прямой A1A2.
Плоскость с пересекает плоскость b по прямой B1B2.
Так как a||b, то и A1A2||B1B2.
Отсюда следует что треугольники PA1A2 и PB1B2 подобны (по трем углам (угол Р - общий, а углы PA1A2 и PB1B2, PA2A1 и PB2B1 равны как соответствующие углы при параллельных прямых))
РА1 : PВ1 = 2:5
РА1 : PВ1=A1A2 : B1B2
2:5=10:B1B2
2B1B2=50
B1B2=25
Приложения:
Автор ответа:
0
Буду благодарна)
Похожие вопросы
Предмет: Информатика,
автор: sl8301321
Предмет: Физика,
автор: lavashek228
Предмет: Русский язык,
автор: mishastadnik091208
Предмет: Обществознание,
автор: katyhovapolina
Предмет: Химия,
автор: Печеньк000