Предмет: Математика,
автор: wotvova99
решить уравнения (даю максимум баллов)
Приложения:
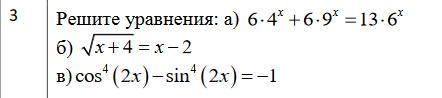
Ответы
Автор ответа:
1
Ответ:
1) x=-1,1
2)x=5
3)
Пошаговое объяснение:
x=0 - посторонний корень
Похожие вопросы
Предмет: Алгебра,
автор: leylassssha
Предмет: Геометрия,
автор: gusenok16
Предмет: Химия,
автор: maksgarbuza
Предмет: Математика,
автор: Каринака1996
Предмет: Математика,
автор: Аноним