Question

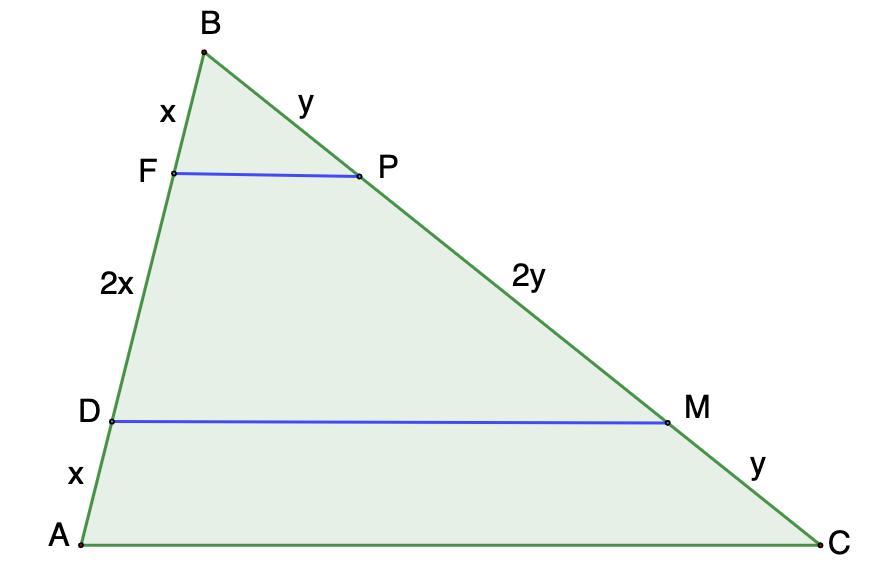
Площа трикутника ABC дорівнює 24 см“. На стороні АВ позначили точ
ки D i F так, що AD = BF = 1:4 AB, а на стороні ВC— точки P i M так
шо СМ = BP = 1:4 вс. Знайдіть площу чотирикутника DFPM.
​

Answer 1

Ответ:

Площадь четырехугольника DFPM равна 12 см².

Объяснение:

Площадь треугольника ABC равна 24 см². На стороне АВ обозначили точки D и F так, что AD = BF = 1/4 AB, а на стороне ВС — точки P и M так, что СМ = ВР = 1/4 ВС. Найдите площадь четырехугольника DFPM.

Дано: ΔАВС;

S (ABC) = 24 см²;

D ∈ AB; F ∈ AB.

AD = BF = 1/4 AB;

P ∈ BC; M ∈ BC;

СМ = ВР = 1/4 ВС.

Найти: S (DFPM)

Решение:

1. Пусть AD = BF = х  ⇒  АВ = 4х, а FD = 2x;

Пусть СМ = ВР = у  ⇒  ВС = 4у, а РМ = 2у.

Тогда BF : FD : DA = x : 2x : x = 1 : 2 : 1;

BP : PM : MC = y : 2y : y = 1 : 2 : 1.

• Если прямые, пересекающие две другие прямые (параллельные или нет), отсекают на обеих из них пропорциональные отрезки, начиная от вершины, то такие прямые параллельны.

⇒ FP || DM || AC.

2. Рассмотрим ΔFBP и Δ АВС.

FP || AC.

• Лемма. Если две стороны треугольника пересекает прямая, параллельная третьей стороне, то она отсекает треугольник, подобный данному.

⇒ ΔFBP ~ Δ АВС.

• Коэффициент подобия k равен отношению сходственных сторон подобных треугольников.

Найдем коэффициент подобия:

$\displaystyle \bf k=\frac{FB}{AB} =\frac{x}{4x} =\frac{1}{4}$

• Отношение площадей подобных треугольников равно квадрату коэффициента подобия.

$\displaystyle \bf \frac{S(FBP)}{S(ABC)}=k^2=\frac{1}{16} \\\\S(FBP)=\frac{S(ABC)}{16}=\frac{24}{16}=1,5\;_{(CM^2)}$

3. Рассмотрим ΔDBM и Δ АВС.

DM || AC.

⇒ ΔDBM ~ Δ АВС.

Найдем коэффициент подобия:

$\displaystyle \bf k=\frac{BD}{AB} =\frac{3x}{4x} =\frac{3}{4}$

Найдем площадь S(DBM):

$\displaystyle \bf \frac{S(DBM)}{S(ABC)}=k^2=\frac{9}{16} \\\\S(DBM)=\frac{S(ABC)\cdot9}{16}=\frac{24\cdot9}{16}=13,5\;_{(CM^2)}$

4. Найдем S(DFPM).

S (DFPM) = S (DBM) - S (FBP) = 13,5 - 1,5 = 12 (см²)

Площадь четырехугольника DFPM равна 12 см².

#SPJ5