Предмет: Алгебра,
автор: fgibhccjvj
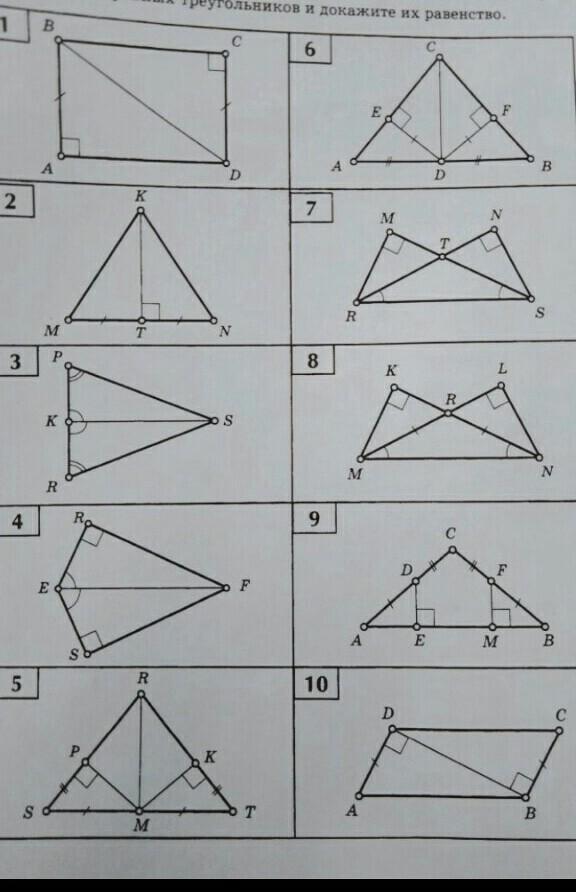
ПОМОГИТЕ ЭТО СРОЧНО! К ЗАВТРАШНЕМУ ДНЮ НАДО!!! найдите пары равных треугольников и докажите их равенства 4—8.
Приложения:
Ответы
Автор ответа:
11
4. Рассмотрим треугольники ERF и ESF Угол R равен углу S и равен 90 градусов. Из этого значит, что ERF - прямоугольный треугольник и ESF - прямоугольный треугольник. По условию EF - гиппотенуза - общая и острые углы REF=SEF
Значит, треугольники ERF и ESF равны по гиппотенузе и острому углу
5. А) Рассмотрим треугольники SPM и TKM
Угол SPM=TKM=90° => треугольник SPM и TKM - прямоугольные. SP=TK (по условию)
SM=TM (по условию)
Из этого следует, что треугольники равны по катету и гиппотенузе
Б) Рассмотрим треугольник PMR и KMR
Угол MPR + угол MPS =180° (смежные углы)
Тогда угол MPR = 180° - угол MPS = 180° - 90° = 90°
Угол MKR + угол MKT = 180°(смежные углы)
Угол MKR = 90° (по аналогии выше)
Угол MPR =углу MKR = 90°
Из этого следует, что треугольники MPR и MKR - прямоугольные
PM = KM (как соответственный элемент из вышедоказанного)
RM - общая
Треугольник PMR =KMR
В) PR=KR (соответственные элементы)
SP=TK (по условию)
SR=SP+PR=TK+KR=RT
Треугольник SRT - равнобедренный
RM - медиана, высота
Угол SMR = угол TMR = 90°
Треугольники SMR и TMR прямоугольные
RM - общая
И они равны по катету и гиппотенузе
6. А) Рассмотрим треугольники CED и CFD
Угол CED=CFD=90°
Треугольники CED, CFD - прямоугольные
ED=FD(по условию)
CD - общая
Они равны по гиппотенузе и катету
Б) Рассмотрим треугольники AED, BFD
По аналогии угол AED =BFD =90°
Треугольники прямоугольные,
AD=BD (по усл.)
ED=FD (по усл.)
И они равны по катету и гиппотенузе
В) AE=BF (как соответственные элементы)
ЕC=FC (как соответственные элементы)
АС=AE+EC=BF+FC=BC
Треугольник ACB - равнобедренный
СD - медиана, высота
Углы ADC = BDC =90°
Треугольники ADC, BDC - прямоугольные
АD=BD (по усл)
CD - общая
Треуг. ADC=BDC по двум катетами
(дальше не буду писать, что тр. прямоугольные, муторно)
7.тр. RMS=SNR по гиппотенузе (RS - общая) и острому углу (углы MSR=NRS)
MR=NS (соотв. элементы)
Уг. МSR=NRS
Тр. RTS - равнобедренный
RT=TS
Тр. MTR=NTS по двум катетам (RT=TS и MR=NS)
8 - точно также, как и 7ой
Значит, треугольники ERF и ESF равны по гиппотенузе и острому углу
5. А) Рассмотрим треугольники SPM и TKM
Угол SPM=TKM=90° => треугольник SPM и TKM - прямоугольные. SP=TK (по условию)
SM=TM (по условию)
Из этого следует, что треугольники равны по катету и гиппотенузе
Б) Рассмотрим треугольник PMR и KMR
Угол MPR + угол MPS =180° (смежные углы)
Тогда угол MPR = 180° - угол MPS = 180° - 90° = 90°
Угол MKR + угол MKT = 180°(смежные углы)
Угол MKR = 90° (по аналогии выше)
Угол MPR =углу MKR = 90°
Из этого следует, что треугольники MPR и MKR - прямоугольные
PM = KM (как соответственный элемент из вышедоказанного)
RM - общая
Треугольник PMR =KMR
В) PR=KR (соответственные элементы)
SP=TK (по условию)
SR=SP+PR=TK+KR=RT
Треугольник SRT - равнобедренный
RM - медиана, высота
Угол SMR = угол TMR = 90°
Треугольники SMR и TMR прямоугольные
RM - общая
И они равны по катету и гиппотенузе
6. А) Рассмотрим треугольники CED и CFD
Угол CED=CFD=90°
Треугольники CED, CFD - прямоугольные
ED=FD(по условию)
CD - общая
Они равны по гиппотенузе и катету
Б) Рассмотрим треугольники AED, BFD
По аналогии угол AED =BFD =90°
Треугольники прямоугольные,
AD=BD (по усл.)
ED=FD (по усл.)
И они равны по катету и гиппотенузе
В) AE=BF (как соответственные элементы)
ЕC=FC (как соответственные элементы)
АС=AE+EC=BF+FC=BC
Треугольник ACB - равнобедренный
СD - медиана, высота
Углы ADC = BDC =90°
Треугольники ADC, BDC - прямоугольные
АD=BD (по усл)
CD - общая
Треуг. ADC=BDC по двум катетами
(дальше не буду писать, что тр. прямоугольные, муторно)
7.тр. RMS=SNR по гиппотенузе (RS - общая) и острому углу (углы MSR=NRS)
MR=NS (соотв. элементы)
Уг. МSR=NRS
Тр. RTS - равнобедренный
RT=TS
Тр. MTR=NTS по двум катетам (RT=TS и MR=NS)
8 - точно также, как и 7ой
Похожие вопросы
Предмет: Английский язык,
автор: ppapapaogo
Предмет: Биология,
автор: dmitrenko162
Предмет: Математика,
автор: burakovaviktoria629
Предмет: Алгебра,
автор: x3m2