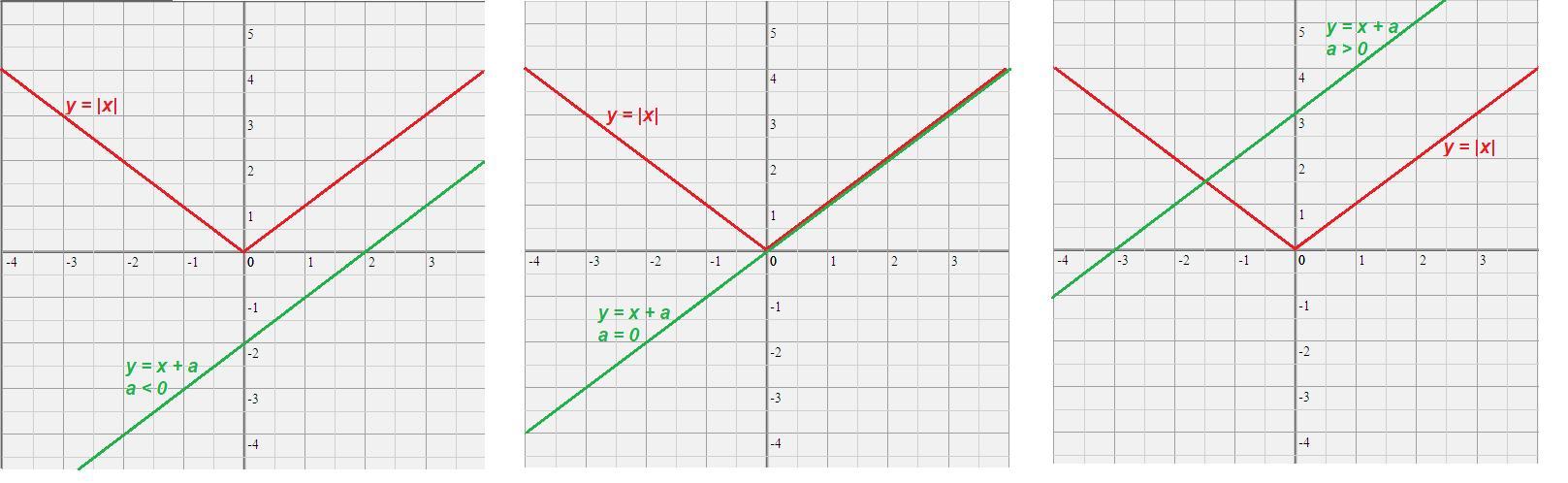
Определите число точек пересечения графиков функций y=|x| и y=x+a для каждого значения числа a.
Ответы
Ответ:
если a < 0, нет точек пересечения,
если а = 0, бесконечно много точек пересечения,
если а > 0. одна точка пересечения.
Объяснение:
Графический метод.
1) Построим график функции у = |x| (красный график)
Так как |x| = x при x ≥ 0, то для x ≥ 0 графиком является луч с началом в точке (0; 0), биссектриса первой координатной четверти.
Так как |x| = - x при x < 0, то для x < 0 графиком является часть прямой у = - х, расположенная во второй координатной четверти.
2) Построим график функции у = х + а (зеленый график) для различных значений а.
Графиком этой функции является прямая, проходящая под углом 45° к положительному направлению оси Ох, и пересекающая ось Оу в точке (0; а).
- Если а < 0, то прямая проходит ниже графика функции у = |x| и не пересекает его.
- Если а = 0, то прямая проходит через начало координат и совпадает с частью графика функции y = |x|, тогда бесконечно много общих точек.
- Если а > 0, то прямая пересекает график функции y = |x| в одной точке.
Аналитический метод:
1) a < 0
|x| = x + a
Если х ≥ 0, то x = x + a
a = 0
но а < 0, значит точек пересечения нет.
Если х < 0, то - x = x + a
- 2x = a
здесь левая часть положительна, правая - отрицательна, значит нет точек пересечения.
2) а = 0
|x| = x
равенство верно, для любых x ≥ 0.
Бесконечно много общих точек.
3) а > 0
Если x ≥ 0, то x = x + a
a = 0
но а > 0, значит точек пересечения нет.
Если x < 0, то - x = x + a
- 2x = a
обе части положительны, значит для каждого а > 0 найдется значение х, при котором равенство будет верно, следовательно одна точка пересечения.