Question

№15 и 16 ( Решить на листочке !!!! )
Даю 35 баллов

Answer 1

Ответ:

Пошаговое объяснение:

Answer 2

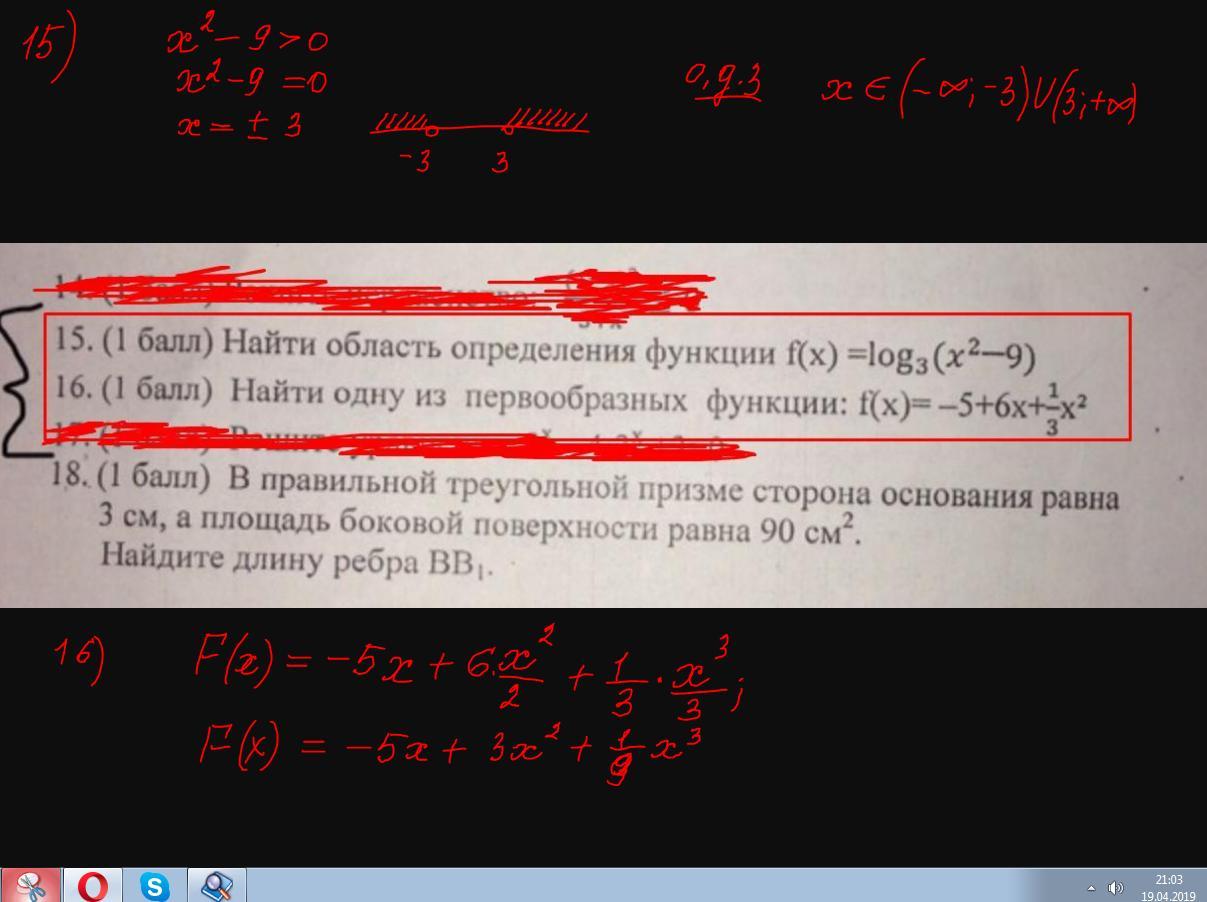
15. Областью определения логарифмической функции будет множество решений неравенства х²-9>0, (х-3)(х+3)>0, Это неравенство решим методом интервалов. Нанесем корни левой части, т.е. числа -3 и 3 на числовую ось, определим те значения х, где левая часть неравенства положительна. Это объединение промежутков (-∞; -3)∪(3;+∞)

16. Одна из первообразных имеет вид

-5х+6х²/2+((1/3)*(х³/3)+с=  -5х+3х²+(х³/9)+с,     где с - любое действительное число. Например, если с=0, то первообразная имеет вид F(х)=-5х+3х²+(х³/3)