Question

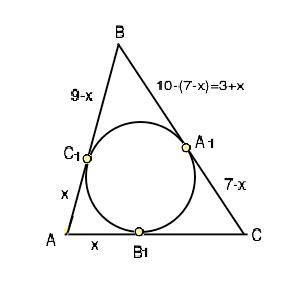
Вписанная в треугольник ABC окружность касается сторон AB, AC, BC в точках C1, B1, A1 соответственно. Известно, что AB=9, AC=7, BC=10. Вычислите длины следующих отрезков.

AC1 BA1 CB1

Answer 1

 Отрезки касательных, проведенных к окружности из одной точки вне её –  равны.

  Примем АС1=х. Тогда АВ1=х, С1В=9-х, В1С=А1С=7-х.

  ВС=10, поэтому ВА1=ВС-А1С=10-(7-х)=3+х. Т.к. ВА1=ВС1, приравняем их значения:

9-х=3+х, откуда 6=2х, ⇒ х=3. Тогда

АС1=3,

ВА1=3+3=6,

СВ1=7-3=4.