Предмет: Алгебра,
автор: David34242342
Помогите пожалуйста !!!!
Приложения:
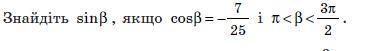
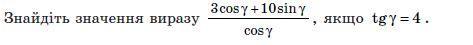
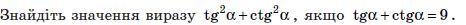
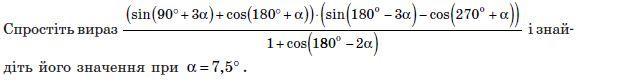
Ответы
Автор ответа:
1
1) α - угол третьей четверти, значит Sinβ < 0
Автор ответа:
1
Ответ:
Объяснение:1)sinβ=±√1-cos²β,β∈3четв.sinβ=-√1-49/625 = -√576/625= -24/25.
2)=3+10tgα=3+10·4=43.(здесь α замени на гамма)
№3)tgα+ctgα=9⇒(tgα+ctgα)²=81
tg²α+2tgα·ctgα+ctg²α=81⇒tg²α+ctg²α=79т.к. tgα·ctgα=1.
4) =(cos3α-cosα)·(sin3α-sinα) /(1-cos2α)=(-2sin2α·sinα)·2cos2α·sinα /2sin²α=
-2sin2α·cos2α= -sin4α=-sin30°=-1/2=-0,5.
Похожие вопросы
Предмет: Қазақ тiлi,
автор: dsm1231
Предмет: Музыка,
автор: spartak070582
Предмет: История,
автор: nazarovaajsa94
Предмет: Литература,
автор: Зима30