Question

Найти минимальное и максимальное значение функции на отрезке
f(x)=5sinx+cos2x [0;n]

Answer 1

$f(x)=5\sin{x}+\cos{2x}\\f'(x)=5\cos{x}-2\sin{2x}$

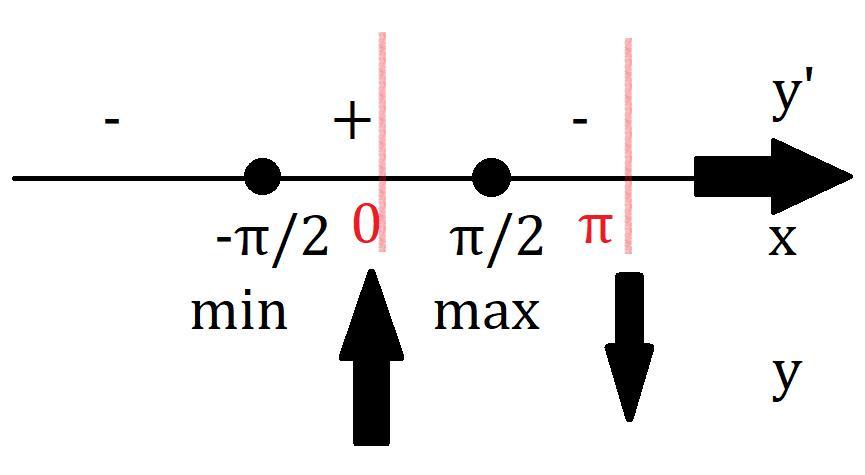
Найдём экстремумы и выделим нужный отрезок.

$f'(x)=4\cos{x}(5/4-\sin{x});|\sin{x}|\leq 1$

Значит экстремумы только в точках cos x =0

Значение в скобке всегда положительное.

См. вниз.

$f(x)_{max}=f(\pi/2)=5-1=4\\f(0)=5*0+1=1;f(\pi)=5*0+1=1=>\\f(x)_{min}=f(0)=f(\pi)=1$

Ответ: Минимальное: 1.

Максимальное: 4.