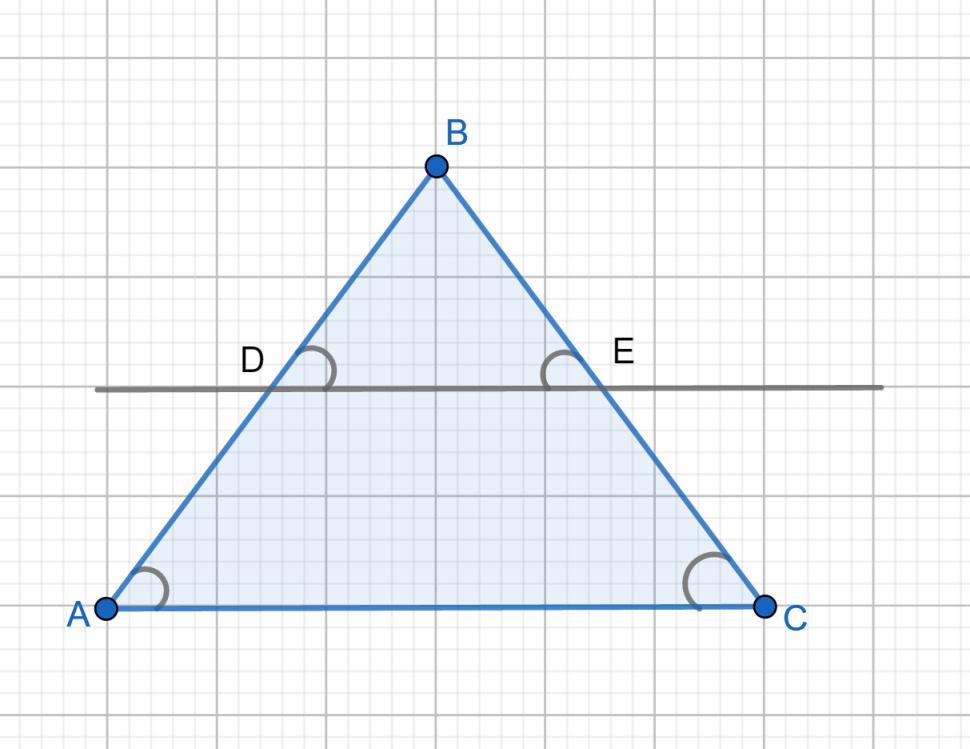
100БАЛЛОВ СРОЧНО. Через середину боковой стороны равнобедренного треугольника проходит прямая, параллельная основанию этого треугольника.Докажите, что эта прямая проходит через середину другой боковой стороны.
Ответы
Можно доказать несколькими способами.
1) По т. Фалеса: Если параллельные прямые отсекают на одной стороне угла равные отрезки, то они отсекают равные отрезки и на второй стороне угла.
Параллельные прямые DE и AC отсекают равные отрезки на стороне AB угла ABC, т.е. AD = DB. Значит на стороне BC они отсекают также равные отрезки BE = EC.
2) Из подобия треугольников. Так как DE ║ AC, то ΔABC подобен ΔDBE по двум углам: ∠B общий, ∠BDE = ∠BAC как соответствующие при DE ║ AC и секущей AB. Так как по условию AD = DB, то BD/AB = 1/2. Коэффициент подобия k = 1/2. ⇒ BE/BC = 1/2, ⇒ BC = 2*BE, тч. E является серединой отрезка ВС.
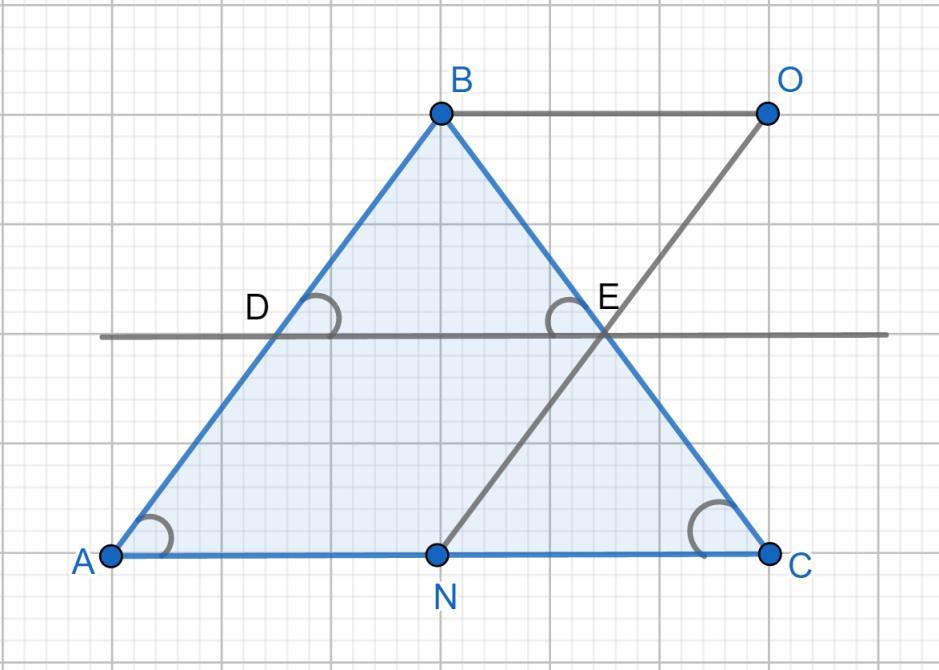
3) Проведем прямые BO ║AC и ON║AB.
DBON параллелограмм, так как его противолежащие стороны параллельны. ⇒ DB = EO. ADEN параллелограмм, так как его противолежащие стороны параллельны, так как AD=DB, то NE=EO.
ΔBEO = ΔNEC по второму признаку: ∠BEO = NEC вертикальные, ∠BOE = ∠ENC внутренние накрест лежащие при BO ║AC и секущей ON. OE = EN. Из равенства треугольников следует BE=EC. ( так доказывается т. Фалеса)