Геометрія 10 клас
( ТЕРМІНОВО і ЛЕГКО )
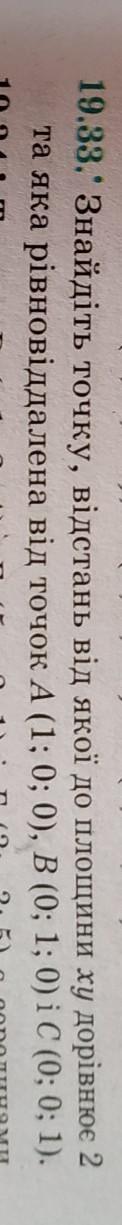
Ответы
Ответ:
Искомая точка М(2;2;2).
Объяснение:
Итак, по условию искомая точка М лежит на расстоянии 2 ед. от плоскости XY, то есть ее координата Z=2. Тогда точка М имеет координаты М(Xm;Ym;2).
Точка М равноудалена от точек А(1;0;0), В(0;1;0) и С(0;0;1), то есть расстояния (модули векторов) равны: |AM|=|BM|=|CM|. Если равны модули, то равны и квадраты модулей. Найдем их по известной формуле:
|AM|²=(Xm-Xa)²+(Ym-Ya)²+(Zm-Za)² = (Xm-1)²+Ym²+4. (1) Аналогично:
|BM|² = (Xm-Xb)²+(Ym-Yb)²+(Zm-Zb)² = Xm²+(Ym-1)²+4. (2)
|CM|² = (Xm-Xс)²+(Ym-Yс)²+(Zm-Zс)² =Xm²+Ym²+(2-1)² = Xm²+Ym²+1. (3).
Приравниваем (2) и (3): Xm²+Ym²+1 = Xm²+Ym²- 2Ym+5 =>
2Ym = 4, Ym =2.
Приравниваем (1) и (2): Xm²-2Xm+1²+Ym²+4 =Xm²+Ym²-2Ym+1²+4. =>
Xm = Ym.
Значит координаты искомой точки М(2;2:2).
Второй вариант (см. рисунок).
Если же нужно решать через уравнения плоскостей и прямых, то:
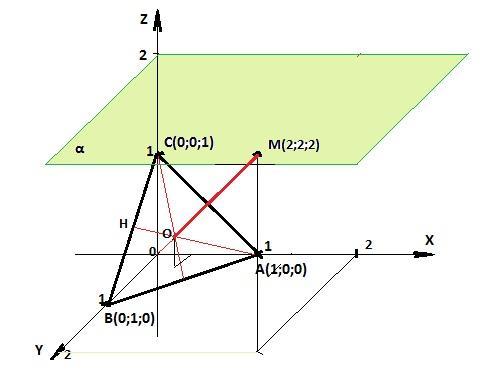
Соединив точки А, В и С, получим равносторонний треугольник АВС, так как его стороны (расстояния между данными точками) равны √2 (по приведенной выше формуле). Центр этого треугольника - центр описанной (вписанной) окружности. Он равноудален от точек А, В и С в плоскости треугольника. Тогда точка М должна лежать на пересечении перпендикуляра к центру треугольника АВС и плоскости α, параллельной плоскости XY
Уравнение плоскости α: Z - 2 = 0 (так как точка М лежит в данной плоскости и, следовательно, плоскость α параллельна плоскости XY. Или в общем виде:
0*x+0*y+z -2 =0, то есть коэффициенты в этом уравнении равны:
А=0, В=0, С=1 и D= -2.
Найдем уравнение плоскости АВС (точки А(1;0;0), В(0;1;0) и С(0;0;1)) и составим уравнение плоскости по формуле:
|X-Xa Xb-Xa Xc-Xa | |X-1 -1 -1 |
|Y-Ya Yb-Ya Yc -Ya | =0 Или |Y-0 1 0 | = 0
|Z-Za Zb-Za Zc-Za | |Z-0 0 1 |
Раскрываем определитель по первому столбцу:
|1 0 | | -1 -1| | -1 -1 |
(X-1)* |0 1| - Y*| 0 1| + Z*| 1 0 | = X - 1 +Y+ Z = 0
Получили уравнение x + y + z -1 =0 c коэффициентами
A= 1, B= 1, C= 1, D= -1.
Теперь найдем координаты центра треугольника АВС.
Так как треугольник АВС равносторонний (по координатам вершин), это центр описанной (вписанной) окружности, лежащий на пересечении медиан треугольника (или, что тоже самое, в точке, делящей медиану в отношении 2:1, считая от вершины).
Найдем координаты конца (точки Н) медианы АН.
Это середина отрезка ВС: Xh = (Xb+Xc)/2 = 0. Yh = (Yb+Yc)/2 =0,5. Zh = (Zb+Zc)/2 = 0,5.
Найдем координаты точки О, делящей отрезок АН в отношении 2:1 (k=2), считая от точки А:
Xo = (Xa+kXh)/(1+k) = (1+0)/3 = 1/3.
Yo=(Ya+kYh)/(1+k) = (0+1)/3 = 1/3.
Zo = (Za+kZh)/(1+k) = (0+1)/3 = 1/3.
Итак, есть точка О(1/3;1/3;1/3), через эту точку надо провести перпендикуляр к плоскости АВС и найти координаты точки пересечения этого перпендикуляра с плоскостью α. Это и будет искомая по условию точка.
Найдем уравнение прямой, проходящей через точку О перпендикулярно плоскости АВС. Уравнение плоскости АВС: x+y+ z - 1 =0. Нормальный вектор этой плоскости: n{1;1;1}. Далее принимаем этот вектор за направляющий вектор искомой прямой, проходящей через точку О и записываем ее уравнение в каноническом виде:
(x-1/3)/1=(y-1/3)/1=(z-1/3)/1.
Осталось найти координаты точки пересечения прямой и плоскости α.
Проще всего это делается с помощью параметрических уравнений прямой:
x =x1+mt, y=y1+nt z=z1+pt, где m=1, n=1, p=1 (соответствующие знаменатели в уравнении прямой). Подставляем эти значения в уравнение плоскости α
(Z - 2 = 0). В нашем случае это только значение
z=z1+pt = 1/3+t:
1/3+t -2 = 0 => t = 5/3 . Тогда координаты точки пересечения прямой и плоскости α: х=1/3 +5/3 = 2. y = 2 и z = 2.
Итак, точка на плоскости α, равноудаленная от точек А, В и С - это точка М(2;2;2).