Предмет: Математика,
автор: Orizz
Доказать используя математическую индукцию для любого n:
Приложения:
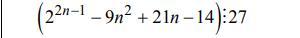
Ответы
Автор ответа:
1
Уточнение: скорее всего, исходное условие звучало так: Доказать, используя математическую индукцию, что утверждение верно для любого натурального n.
Пошаговое объяснение:
1) n = 1:
Верно
2) Пусть для n = k
3) Докажем условие для n = k + 1:
Доказано.
Похожие вопросы
Предмет: Русский язык,
автор: lenalena481552
Предмет: Химия,
автор: mkvika2008
Предмет: Математика,
автор: lenurovalana
Предмет: Алгебра,
автор: marfa2307
Предмет: История,
автор: Аноним