Подробное решение плиз
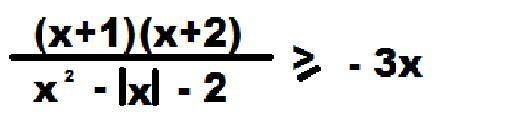
Ответы
(х+1)(х+2)/(х²- |x| -2) ≥ -3х
Решение:
Будем снимать знак модуля, учитывая его определение:
|x| = x при х ≥0 и |x| = -x при х < 0
так что будем эти 2 варианта рассматривать.
1) х ≥ 0
(х+1)(х+2)/(x² -x -2) ≥ -3x х ≠ -1, х ≠ 2
(х+1)(х+2)/(x² -x -2) + 3x ≥ 0
((x+1)(x+2) +3x(x² -x -2) )/(x² -x -2) ≥ 0
((x+1)(x+2) +3x(x +1)(x -2) )/(x² -x -2) ≥ 0
(x+1)(x +2 +3x(x-2) ) / (x² -x -2) ≥ 0
(х +1)(х +2 +3х²-6х) / (х+1)(х-2) ≥ 0
(3х²-5х +2)/(х-2) ≥ 0
3(х -1)(х-2/3) / (х-2) ≥ 0
(х -1)(3х -2)/(х -2) ≥ 0
корни 1, 2/3 и 2
-∞ 2/3 1 2 +∞
+ - + + это знаки (х -1)(3х -2)
- - - + это знаки (х -2)
IIIIIIIIIIIIIIII IIIIIIIIIIIIIIIIIII это решение нер-ва
Ответ: х∈ [2/3; 1)∪(2; +∞)
2) х < 0
(х+1)(х+2)/(x² +x -2) ≥ -3x х ≠ 1, х ≠- 2
(х+1)(х+2)/(x² +x -2) + 3x ≥ 0
((x+1)(x+2) +3x(x² +x -2) )/(x² +x -2) ≥ 0
((x+1)(x+2) +3x(x -1)(x +2) )/(x² +x -2) ≥ 0
(x+2)(x +1 +3x(x-1) ) / (x² +x -2) ≥ 0
(х +2)(х +1 +3х²-3х) / (х-1)(х+2) ≥ 0
(3х²-2х +1)/(х-1) ≥ 0
(х-1) ≥ 0
х > 1
C учётом условия, что х < 0 и х > 1 решения нет.
Так что
Ответ:х∈ [2/3; 1)∪(2; +∞)