Предмет: Алгебра,
автор: akvaro
объясните, пожалуйста, как выполнено преобразование, где 1+ sin фи+ cos фи
Приложения:
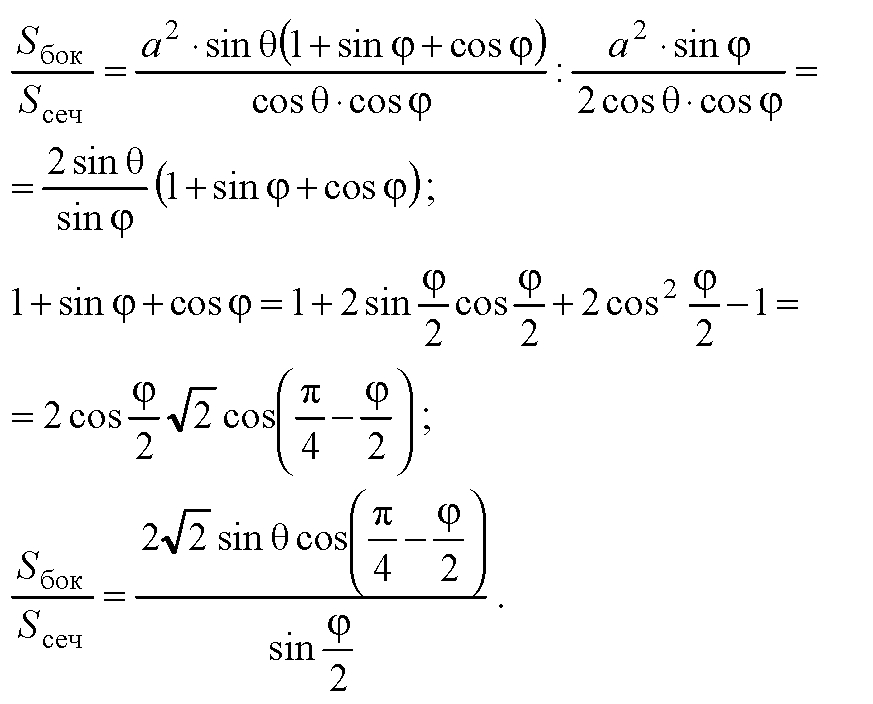
Ответы
Автор ответа:
0
Если выполнишь деление, получишь


Так понятно? Я только заменила "фи" на α, а "тэта" на β, не смогла эти буквы через редактор формул напечатать.
Во втором случае после вынесения 2cos^2(φ/2) остается (sin(φ/2) +cos(φ/2)), эта сумма по формуле равна √2 сos(π/4-φ/2).
Так понятно? Я только заменила "фи" на α, а "тэта" на β, не смогла эти буквы через редактор формул напечатать.
Во втором случае после вынесения 2cos^2(φ/2) остается (sin(φ/2) +cos(φ/2)), эта сумма по формуле равна √2 сos(π/4-φ/2).
Автор ответа:
0
единицы сокращаются, выносишь косинус фи пополам за скобку ,получается сумма синуса и косинуса, искусственно умножаешь синус на корень из двух и делишь на корень из 2, чтобы ничего не изменилось, с косинусом в скобках проделываешь то же самое, потом корень из двух выносишь за скобку, а в скобках и у того и у другого остаётся 1/корень из 2, а корень из 2 около синуса записываешь как синус пи на 4, а около косинуса 1/корень из 2 записываешь как косинус пи на 4 и всё что в скобках складываешь по формуле разности углов cos α · cos β + sin α · sin β=cos(α – β)
Приложения:

Похожие вопросы
Предмет: Химия,
автор: arinaantip2008
Предмет: География,
автор: Аноним
Предмет: Обществознание,
автор: Vudachinaz
Предмет: Математика,
автор: annashamina
Предмет: Литература,
автор: zhenya97w