Question

Допоможіть!!!!!! Будь ласка!!!!!!
Знайти довжину кола вписаного в ромб діагоналі якого 15 і 20 см
Терміново!!!!!
​

Answer 1

Ответ:

L = 2π·R = 12π.

Объяснение:

Найти длину окружности, вписанной в ромб, диагонали которого равны 15см и 20см.  

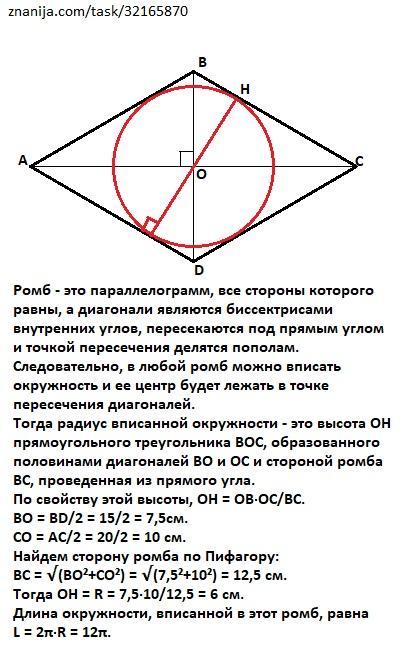
Ромб - это параллелограмм, все стороны которого равны, а диагонали являются биссектрисами внутренних углов, пересекаются под прямым углом и точкой пересечения делятся пополам. Следовательно, в любой ромб можно вписать окружность и ее центр будет лежать в точке пересечения диагоналей.

Тогда радиус вписанной окружности - это высота ОН прямоугольного треугольника ВОС, образованного половинами диагоналей ВО и ОС и стороной ромба ВС, проведенная из прямого угла.

По свойству этой высоты, ОН = ОВ·ОС/ВС.

ВО = BD/2 = 15/2 = 7,5cм.

СО = АС/2 = 20/2 = 10 см.

Найдем сторону ромба по Пифагору:

ВС = √(ВО²+СО²) = √(7,5²+10²) = 12,5 см.

Тогда ОН = R = 7,5·10/12,5 = 6 см.

Длина окружности, вписанной в этот ромб, равна

L = 2π·R = 12π.