Предмет: Математика,
автор: Аноним
СРОЧНО развязать интеграл(интегрування дифференцированням бинома) ОТ РУКИ НА ЛИСТКЕ
Приложения:
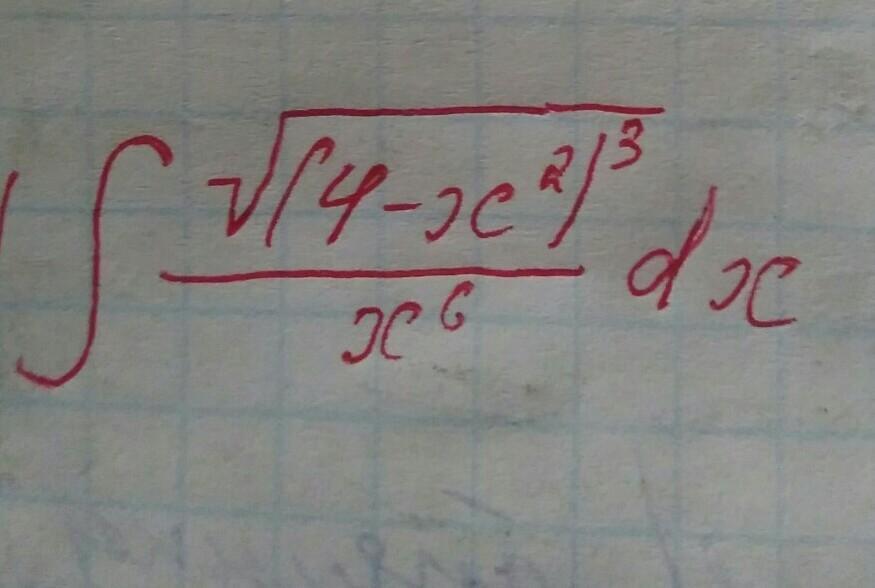
Ответы
Автор ответа:
1
Похожие вопросы
Предмет: Химия,
автор: karolinakvlk
Предмет: Информатика,
автор: kanekoaoy
Предмет: География,
автор: lyudmilasc20mil
Предмет: Математика,
автор: дмитрий244