Предмет: Математика,
автор: шахмарданов
Вычислить определённый интеграл
Приложения:
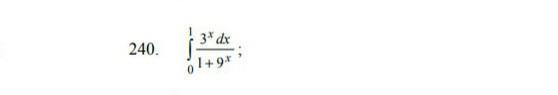
Ответы
Автор ответа:
1
Внесли 3^х под знак дифференциала. Получили табличный интеграл (арктангенс). Применили формулу Ньютона-Лейбница.
Похожие вопросы
Предмет: Русский язык,
автор: Revoution3877
Предмет: Математика,
автор: bsubeedi000gmailcom
Предмет: Английский язык,
автор: 3617642015pasha
Предмет: Биология,
автор: ekaterinamenza