Question

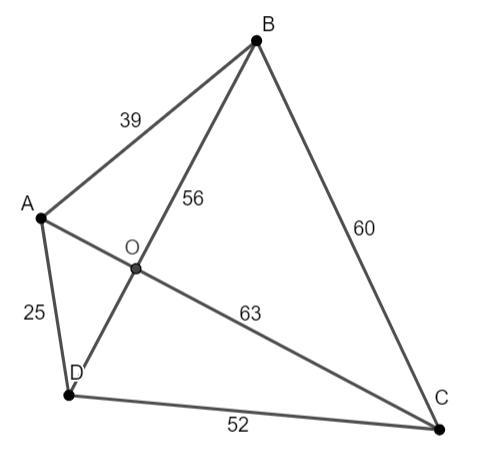
На плоскости даны точки A, B, C, D, причём AB=39, BC=60, CD=52, AD=25, AC=63, BD=56. Какое наименьшее значение может принимать сумма OA+OB+OC+OD для произвольной точки O плоскости?

Answer 1

OA+OB+OC+OD = (OA+OC)+(OB+OD)

Если два значения минимальны, то и их сумма минимальна.

Если сумма расстояний OA+OC минимальна, то O лежит на отрезке АС.

Если сумма расстояний OB+OD минимальна, то О лежит на отрезке BD.

Получаем, что при минимальной сумме OA+OB+OC+OD, О=AC∩BD.

Тогда OA+OB+OC+OD = AC+BD = 63+56 = 119

Ответ: 119.