Question

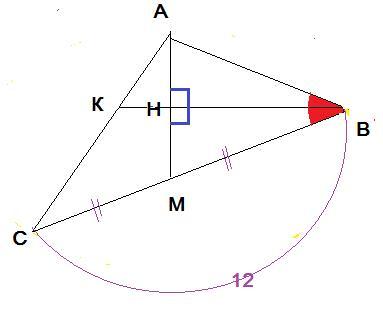
Медиана AM треугольника ABC перпендикулярна его биссектрисе BK. Найдите AB, если BC=12.

Answer 1

Ответ:  АВ=6

Объяснение:  По признаку равенства прямоугольных треугольников (если катет и острый угол одного прямоугольного треугольника соответственно равны катету и острому углу другого прямоугольного треугольника, то такие треугольники равны)  ΔАНВ=ΔМНВ, так как

катет ВН-общий, ∠АВН=∠НВМ ⇒ ∠ВАН=∠ВМН⇒

ΔМАВ-равнобедренный,  АВ=МВ, МВ=СВ/2=12/2=6 ( по условию-АМ-медиана)⇒

АВ=6