Предмет: Алгебра,
автор: Koteno4ek2017
Помогите доказать тождества
Приложения:
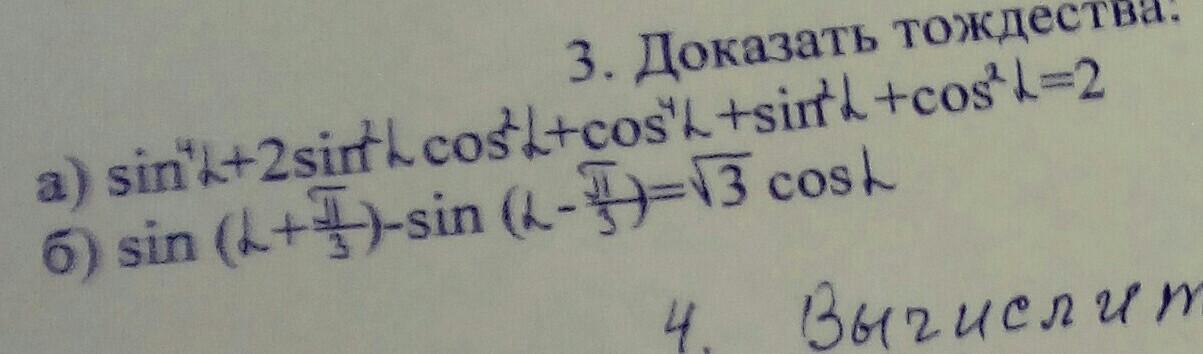
Ответы
Автор ответа:
1
a) Sin⁴α + 2Sin²αCos²α + Cos⁴α + Sin²α + Cos²α =
= (Sin⁴α + 2Sin²ααCos² + Cos⁴α) + (Sin²α + Cos²α) =
= (Sin²α + Cos²α)² + (Sin²α + Cos²α) = 1² + 1 = 2
2 = 2
Тождество доказано
б)
Тождество доказано
Похожие вопросы
Предмет: Английский язык,
автор: mindrinanasta
Предмет: Литература,
автор: Аноним
Предмет: Математика,
автор: danilovazoek
Предмет: Математика,
автор: SOROCINALIZA
Предмет: Биология,
автор: 453553