Решите неравенство пожалуйста
Ответы
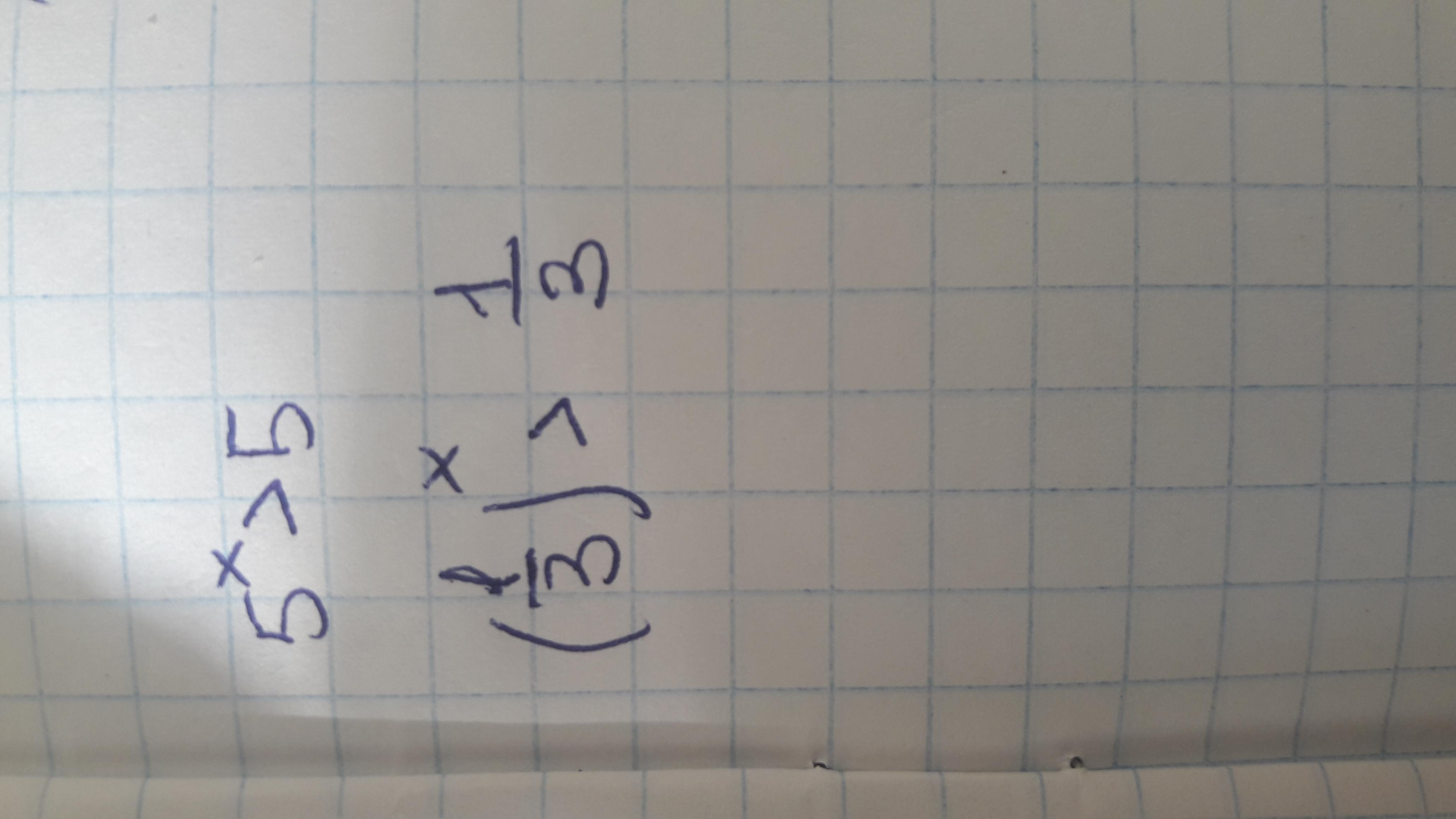
5ˣ > 5,
5ˣ > 5¹,
Т.к. функция f(x) = 5ˣ является строго возрастающей, поэтому большему значению аргумента соответствует большее значение функции, т.е.
x₁ > x₂ => f(x₁) > f(x₂).
То есть, из 5ˣ > 5¹, следует x>1. Доказывается от противного: если бы
было x≤1, тогда (по определению строго возрастающей функции) получили бы 5ˣ ≤ 5¹, что противоречит нашему: 5ˣ > 5¹.
Ответ. x>1.
(1/3)ˣ > (1/3),
(1/3)ˣ > (1/3)¹
Функция f(x) = (1/3)ˣ является строго убывающей, поэтому большему значению аргумента соответствует меньшее значение функции, то есть
x₁ > x₂ => f(x₁) < f(x₂).
Тогда получаем, x<1. Доказывается от противного: если бы было x≥1, тогда по определению строго убывающей функции мы бы имели
(1/3)ˣ ≤ (1/3)¹, что противоречит тому, что (1/3)ˣ > (1/3)¹.
Поэтому x<1.
Можно поступить и по другому: (1/3)ˣ > (1/3), <=> 3^(-x) > 3^(-1),
и теперь, т. к. g(x) = 3ˣ, является строго возрастающей функцией, то получаем (-x) > -1, <=> x<1.
Ответ. x < 1.
Замечание. Функция f(x) = aˣ это показательная функция, является строго убывающей при 0<a<1; и она же является строго возрастающей при a>1.