Предмет: Алгебра,
автор: БердниковаСонечка
Помогите побыстрее пожалуйста! Даю 50 баллов!
Приложения:
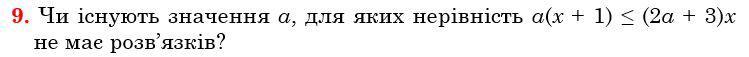
Ответы
Автор ответа:
3
При каких а неравенство не будет иметь решения?
Выразим переменную х через параметр а
Рассмотрим несколько случаев
1) при а= -3
подставим а= -3 в наше неравенство
Данное неравенство справедливо для любого х
Значит:
при а= -3 решением будет х∈R
при a> -3 решением будет x≥a/(a+3)
при a< -3 решением будет x≤a/(a+3)
и нет таких значений а - где неравенство не будет иметь решений
antonovm:
есть ошибка в вашем решении : x (a +3) > a , во-первых делить на ( a + 3 ) нельзя , надо сначала проверить а = -3 , убедиться , что это значение подходит , затем рассмотреть а не равное -3 , во - вторых , вы же не знаете знак ( а+3) , непонятно тогда почему решением будет x > a /( a+3) , а если (а+3 ) отрицательно ?
проверка при а= -3 проведена
x (a +3) => a по условию. Не вижу ошибки
знак неравенства будет другим , если ( а +3) отрицательно
и вы сначала делите , а потом проверяете , а надо наоборот
хорошо.. это исправила
теперь все замечательно !
Похожие вопросы
Предмет: Математика,
автор: ilyasaltyn183
Предмет: Математика,
автор: ikromzakirov5
Предмет: Русский язык,
автор: slowwing
Предмет: Математика,
автор: 09065
Предмет: Математика,
автор: vunyabelka