Предмет: Математика,
автор: lolike
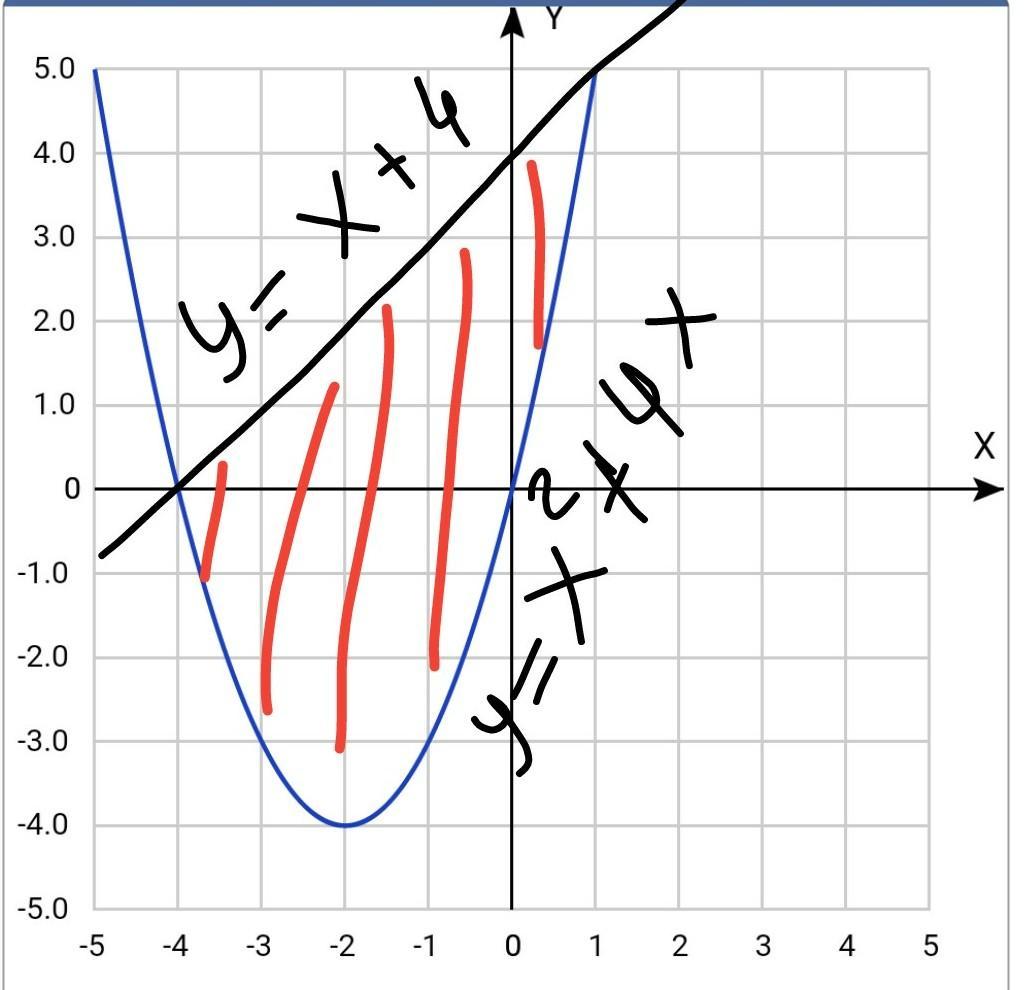
Вычислить площадь, ограниченную линиями: y=x^2+4x, y=x+4
Ответы
Автор ответа:
0
Найдем точки пересечения графиков:
по теореме Виета найдем корни уравнения
*интеграл от -4 до 1
Ответ в кв.ед:
или
Приложения:
Похожие вопросы
Предмет: Українська література,
автор: Аноним
Предмет: Биология,
автор: batarelocka002
Предмет: Английский язык,
автор: Kyk83o2
Предмет: Геометрия,
автор: muhorin2014
Предмет: Геометрия,
автор: nazico14