Question

Найдите диаметр окружности, вписанной в равнобедренную
трапецию, если сумма оснований трапеции равна 15, а разность
оснований равна 9

Answer 1

По условию составим систему уравнений и решим ее.

b + a = 15

b - a = 9

сложим уравнения: 2b = 24; b = 12; ⇒ a = 3. Основания трапеции 12 и 3.

В трапецию вписана окружность, значит суммы противоположных сторон равны. a + b = m + n = 15.

Трапеция равнобедренная. ⇒ m = n = 15/2 = 7,5

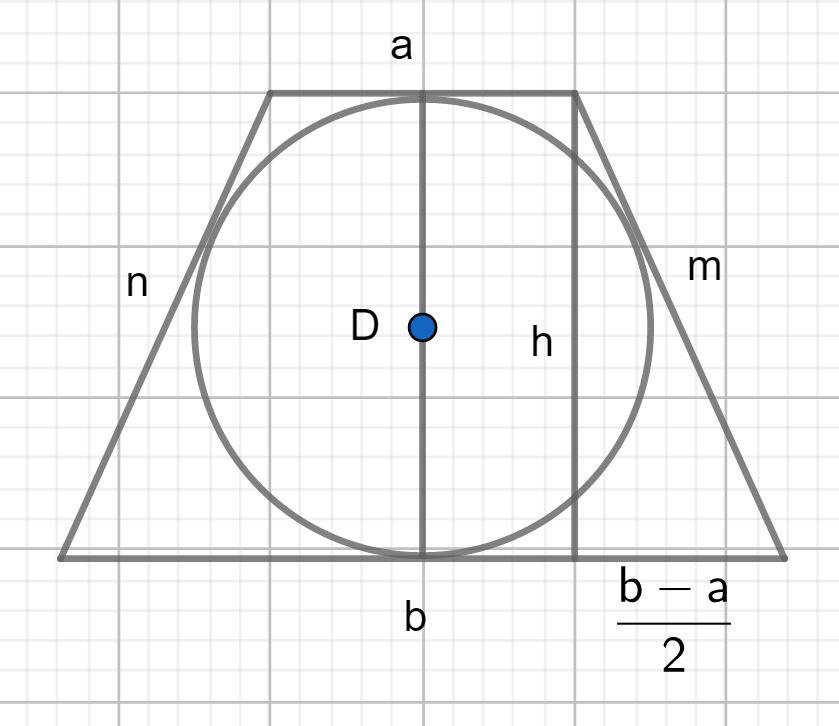
Диаметр вписанной окружности равен высоте трапеции D = h.

В прямоугольном треугольнике гипотенуза = m = 7,5; меньший катет = (b-a)/2 = 4,5; больший катет равен высоте трапеции и диаметру вписанной окружности.

По т. Пифагора: D = h = √(7,5² - 4,5²) = 6

Диаметр вписанной окружности = 6.