Предмет: Геометрия,
автор: щербинен
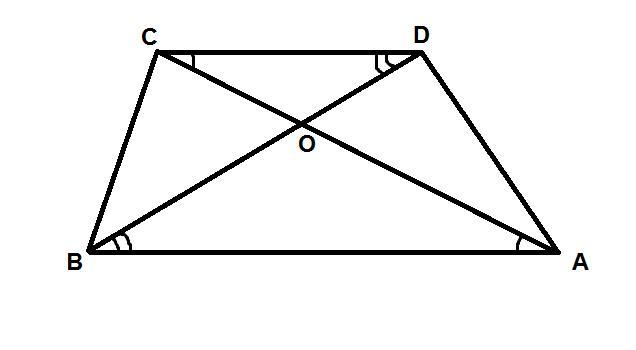
Диагонали трапеции ABCD с основаниями AB и DC пересекаются в точке O. Периметры треугольников ABO и DOCотносятся как 3 : 2 BD=30 см. Найдите длины отрезков BO и OD.
Ответы
Автор ответа:
1
Решение:
Так как AB║DC (как основания трапеции ABCD), то ∠АВD=∠CBD и ∠BAC=∠DCA как накрест лежащие.
Отсюда ΔАВО подобен ΔDOC по 2-ум углам.
Отношение периметров подобных треугольников равно коэффициенту подобия ⇒ k=PΔABO/PΔDOC=3/2
BO/OD=3/2 ⇒ BO=3/2 OD
BD=BO + OD=30 см
5/2 OD=30 см
OD=30 см × 2/5=12 см
ВО=3/2 OD=3/2 × 12 см=18 см
Ответ: 18 см и 12 см
Приложения:
Похожие вопросы
Предмет: Информатика,
автор: eriklit
Предмет: Русский язык,
автор: iliavirsta
Предмет: Алгебра,
автор: arembin
Предмет: Литература,
автор: LA31012000
Предмет: Биология,
автор: ZakAbdulaziz