Предмет: Геометрия,
автор: andreykoptyaev893
1. Дан куб
ABCDA1B1C1D1 , длина ребра которого равна a. На ребре AA1 взята точка E
так, что AE a/4. Найти объём пирамиды, вершиной которой является точка
A1, а основанием – сечение куба, проходящее через точки D и E, и произвольную внутреннюю точку ребра BB1.
berianidzelukap9wyc8:
Ответ в книге есть?
а у Вас какой ответ?
Ответа нет
да,я не Вас спрашиваю:)
четвертая часть куба , задача устная
Ответы
Автор ответа:
2
Решение : /////////////////////////////////
Приложения:
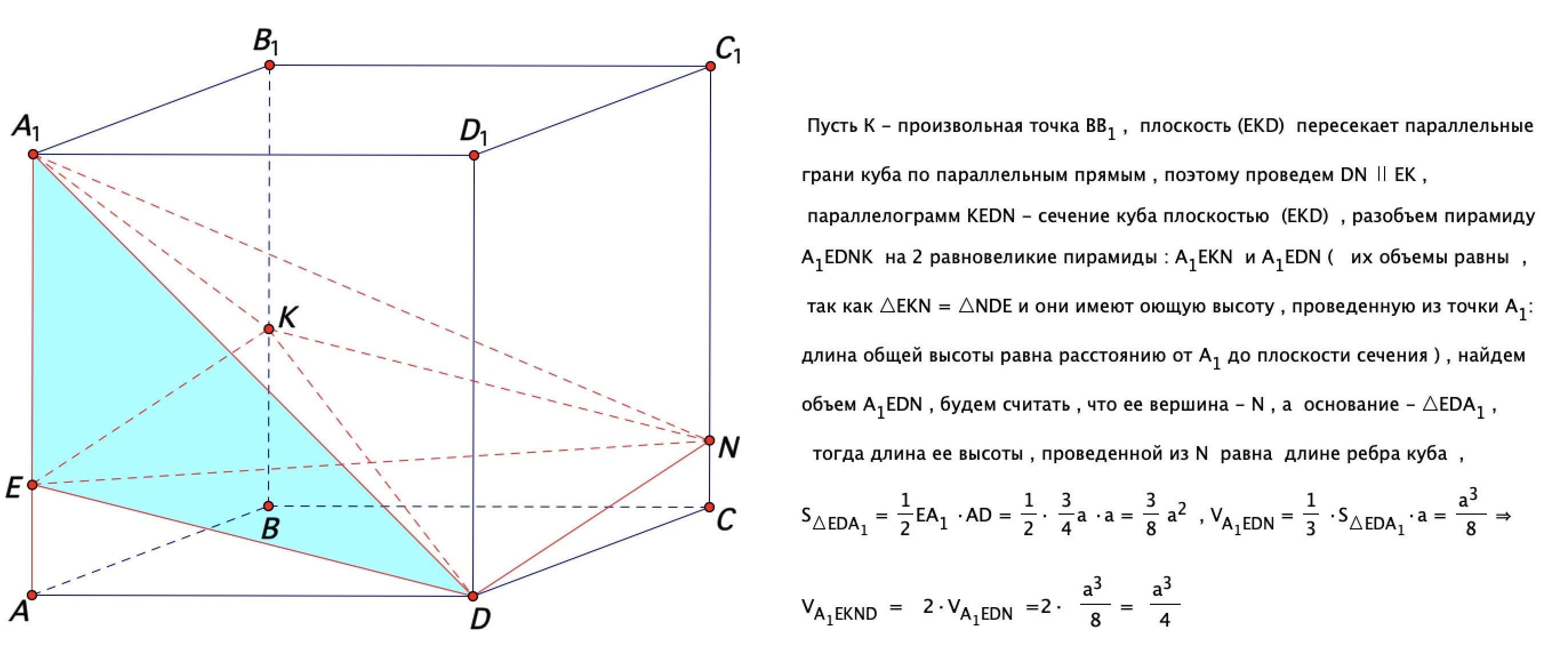
Почему высота, проведенная из точки N, равна ребру куба?
прямая СС1 параллельна DD1 и значит параллельна плоскости ADD1 , а тогда расстояние от точки N до этой грани равно расстоянию от точки С до этой грани , то есть ребру куба
Похожие вопросы
Предмет: Английский язык,
автор: syrlybajmagzan0
Предмет: Русский язык,
автор: dfghyujink23jink
Предмет: Математика,
автор: diakonovaanna230120
Предмет: Физика,
автор: laska06464
Предмет: Математика,
автор: milenasalikova