Предмет: Математика,
автор: bmopi
Найти приделы функции
Приложения:
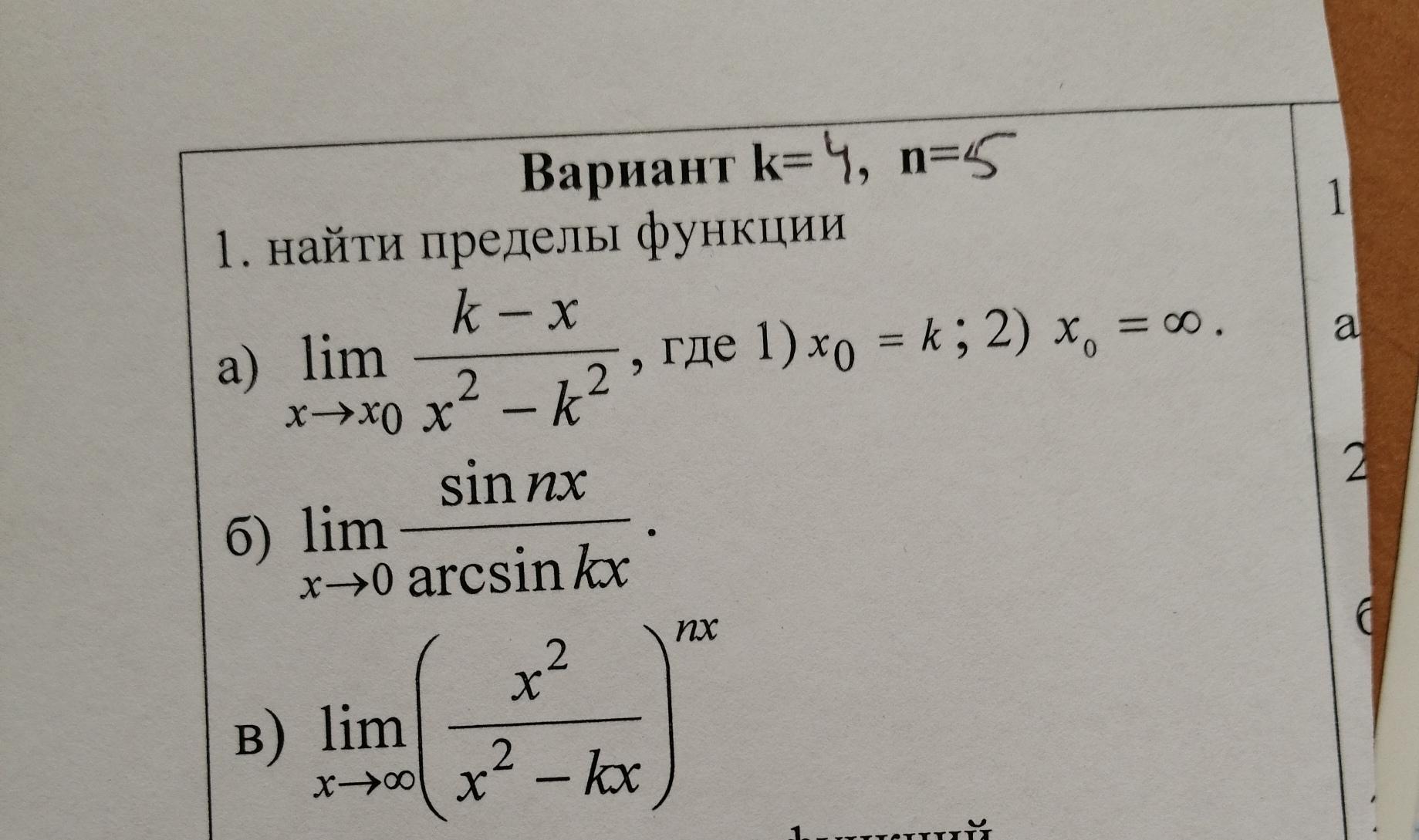
Ответы
Автор ответа:
0
1.а.1 при х ->к
при х -> беск
1 а 2
1б
bmopi:
спасибо, конечно чуть бы пораньше)
как увидел)
Похожие вопросы
Предмет: Геометрия,
автор: timgg2000
Предмет: Биология,
автор: zinovyv07
Предмет: Математика,
автор: pejtonmuamer91
Предмет: Алгебра,
автор: evashabaevamadr
Предмет: Литература,
автор: likeller