Предмет: Математика,
автор: nargiz34
Как решаются примеры типа 84. Прошу объясните
Приложения:
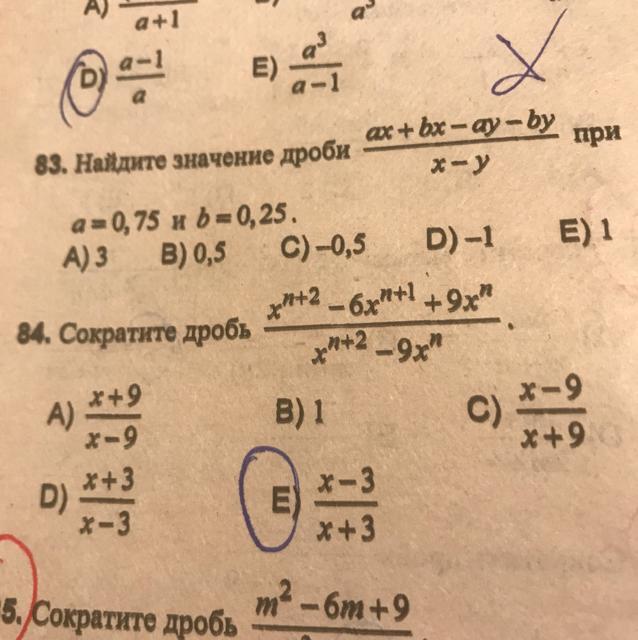
Ответы
Автор ответа:
1
Используем формулы сокращенного умножения:
Ответ: Е
Похожие вопросы
Предмет: Математика,
автор: golovejdmitro4
Предмет: Українська мова,
автор: bogdanab532
Предмет: Химия,
автор: dn7703
Предмет: Литература,
автор: Lukindanja
Предмет: Алгебра,
автор: Em23