Предмет: Алгебра,
автор: КиСа009
При каких значениях параметра а система имеет хотя бы одно решение?
Приложения:
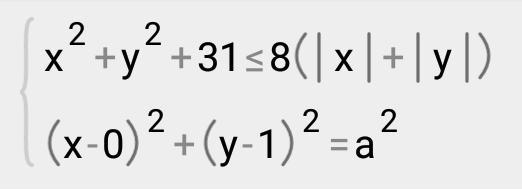
Ответы
Автор ответа:
0
рассмотрю случай когда х и у положительны
x^2+y^2-8x-8y+31≤0
(x-4)^2+(y-4)^2-1≤0
(x-4)^2+(y-4)^2≤1-это круг радиуса 1 с центом в точке О(4;4)
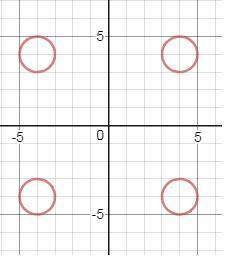
учитывая разные знаки х и у -графиком первого уравнения будут четыре круга-рисунок 1
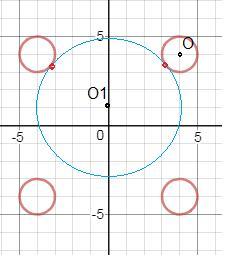
второе уравнение-это уравнение окружности радиуса а с центром в О1(0;1)
решением системы будет 2 точки, пересечение окружности с центром в О1 и окружности с центром в О.(симметричный круг с центром в О2(-4;4) даст вторую точку, радиус а будет такой же-поэтому я рассмотрю первый случай)
Чтобы найти а, посчитаю расстояние ОО1 и вычту из него 1(радиус круга)
OO1^2=(4-0)^2+(4-1)^2=16+9=25
OO1=5
тогда a=5-1=4
учитывая что параметр -просто число, а не радиус окружности, то случай a=-4 тоже подойдет
при а=+-4 у системы будет 2 решения
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: abylaizhunus
Предмет: Английский язык,
автор: karinaserpokrylenko8
Предмет: Химия,
автор: ellis104
Предмет: Математика,
автор: wariox75
Предмет: Геометрия,
автор: коля2018