Предмет: Алгебра,
автор: asdfghjkl1605
как решать показательные неравенства?
Приложения:
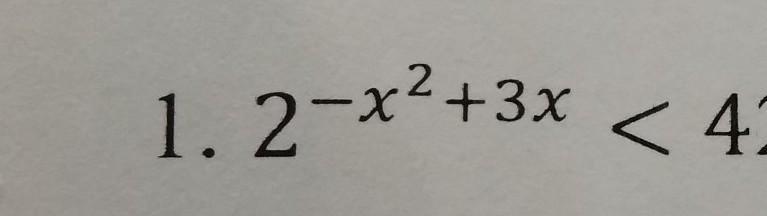
ponacakir:
полностью пример сфоткай
он полность сфоткан. дальше цифра 2 следующего примера
Ответы
Автор ответа:
1
т.к. - показательная функция, основание больше 1, т.е. 2>1.
То знак НЕ меняется.
Введём функцию: квадратичная функция, график парабола, ветви вверх, т.к. коэффициент при
2) Найдём область определения функции:
3) Найдём корни уравнения, т.е.
Решая методом интервалов, находим, что решение выглядит так:
Секундочку, сейчас поменяю кое-что
не совсем полностью расписал
Всё
Похожие вопросы
Предмет: Музыка,
автор: Аноним
Предмет: Українська література,
автор: pogoriliymark
Предмет: Математика,
автор: pro090
Предмет: Математика,
автор: polinanikifor