Напишите уравнение касательно проведенной к графику функции
1) f(x)=x^2-2x-3 x0=2
2) f(x)=4-x x0=-1
3) f(x)=3+2x-x^2 x0=-2
Ответы
Где у - уравнение касательной, f-функция, x₀-точка функции, f'-производная от функции.
1)
2)
3)
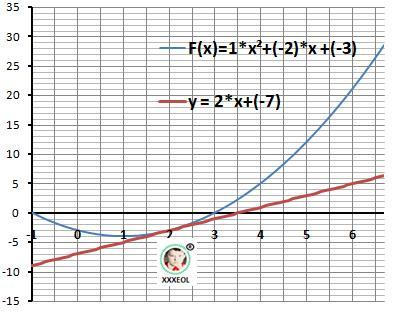
1, Дано: F(x) = x²-2*x -3 - функция, Хо = 2.
Найти: Уравнение касательной.
Решение.
Y = F'(Xo)*(x - Xo) + F(Xo) .
Находим первую производную - k - наклон касательной.
F'(x) = 2*x -2.
Вычисляем в точке Хо = 2.
F'(2) = 2 - производная и F(2) = -3 - функция.
Записываем уравнения прямой.
Y = 2*(x - 2) -3 =
Рисунок к задаче в приложении.
y =2*x -7 - касательная - ОТВЕТ
2. Дано: F(x) = 4 - x, Xo = -1
Это уравнение прямой - касательной не может быть, она просто совпадает с функцией.
y = 4 - x - касательная - ОТВЕТ
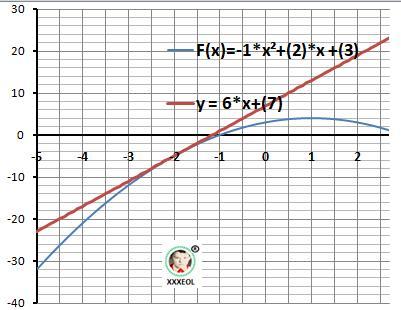
3, Дано: F(x)= - x²+2*x +3 - функция, Хо = -2.
Найти: Уравнение касательной.
Решение.
Y = F'(Xo)*(x - Xo) + F(Xo) .
Находим первую производную - k - наклон касательной.
F'(x) = -2*x + 2.
Вычисляем в точке Хо = -2.
F'(-2) = 6 - производная и F(-2) = -5 - функция.
Записываем уравнения прямой.
Y = 6*(x - (-2) -5) = y = 6*x + 7 - касательная - ОТВЕТ
Рисунок к задаче в приложении.