Question

Вариант I
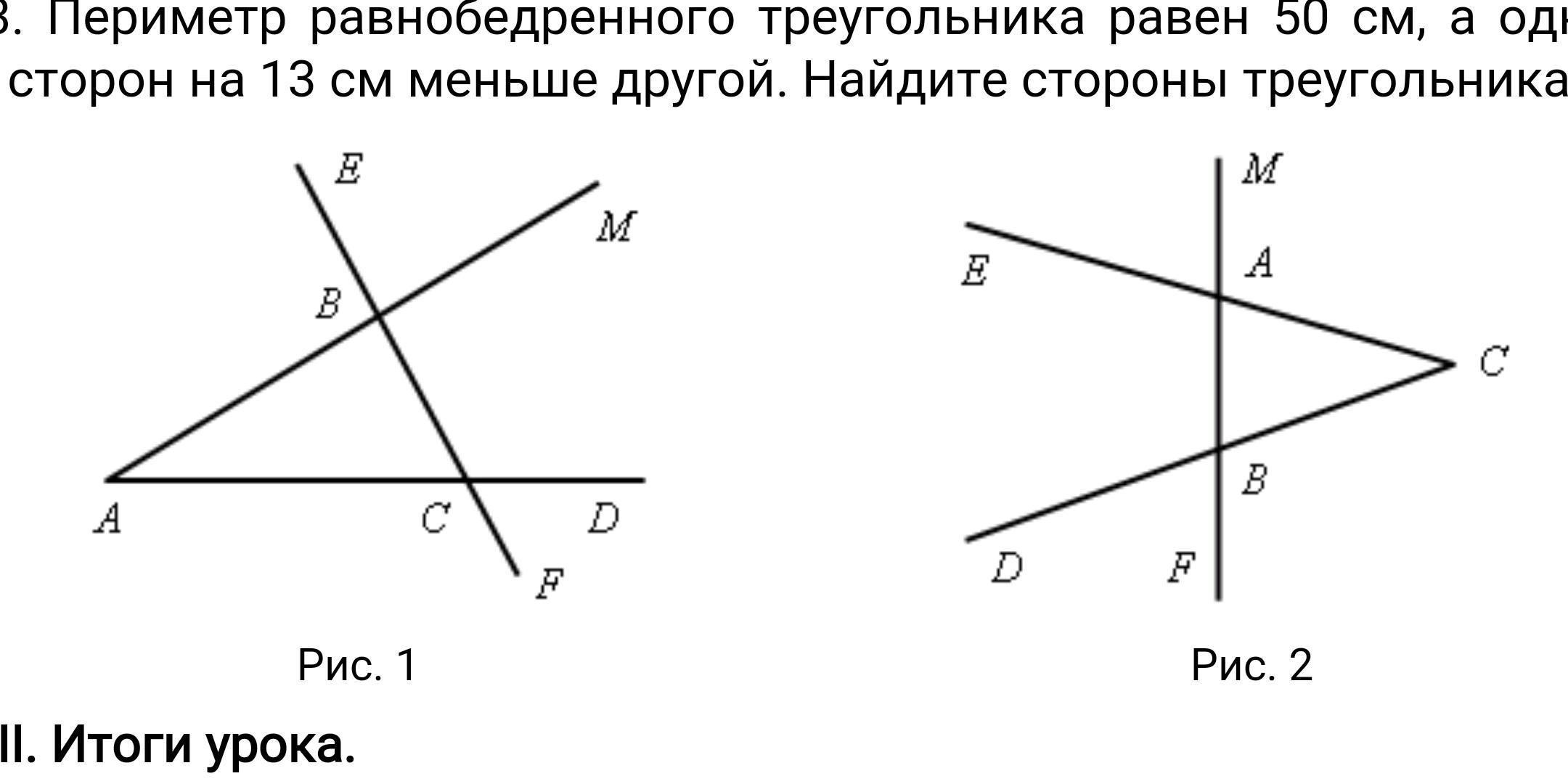
1. На рисунке 1 АВЕ = 104°, DСF = 76°, АС = 12 см. Найдите сторону АВ треугольника АВС.
2. В треугольнике СDЕ точка М лежит на стороне СЕ, причем СМD острый. Докажите, что DЕ > ДМ.
3. Периметр равнобедренного тупоугольного треугольника равен 45 см, а одна из его сторон больше другой на 9 см. Найдите стороны треугольника.
Вариант II
1. На рисунке 2 ВАЕ = 112°, DВF = 68°, ВС = 9 см. Найдите сторону АС треугольника АВС.
2. В треугольнике MNP точка K лежит на стороне MN, причем NKP острый. Докажите, что KР < МР.
3. Одна из сторон тупоугольного равнобедренного треугольника на 17 см меньше другой. Найдите стороны этого треугольника, если его периметр равен 77 см.
Вариант IV
(для более подготовленных учащихся)
1. На рисунке 2 ЕАМ = DВF; ВС = 17 см, РАВС = 45 см. Найдите сторону АВ треугольника АВС.
2. В треугольнике СDЕ Е = 76°, D = 66°, ЕK – биссектриса треугольника. Докажите, что KС > DK.
3. Периметр равнобедренного треугольника равен 50 см, а одна из его сторон на 13 см меньше другой. Найдите стороны треугольника.

Answer 1

АВЕ = 104° Следовательно АВС=76 (смежные углы)

, DСF = 76° следовательно АСВ=76 (вертикальные)

САВ- равнобедренный треугольник

АС = АВ= 12 см.

2.В треугольнике СDЕ точка М лежит на стороне СЕ, причем СМD острый

Значит, DМЕ -тупой (смежные углы) и самый большой в треугольнике ЕМD. Против большего угла лежит большая сторона. Следовательно, DE>DM. Что и требовалось доказать

Периметр равнобедренного тупоугольного треугольника равен 45 см, а одна из его сторон больше другой на 9 см. Найдите стороны треугольника.

а-сторона,  а+9 - основание треугольника

а+а+а+9=45

3а= 36

Стороны треугольника равны: а=12        а+9=21

12+12+21= 45