Question

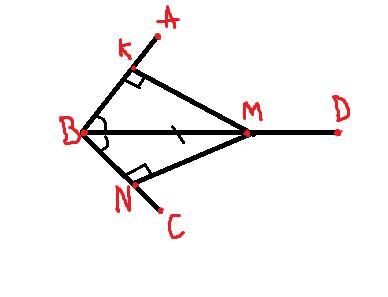
Из точки М,лежащей на биссектрисе BD угла ABС опущены перпендикуляры MK и MN на стороне угла.Докажите, что BK=BN.Найдите BK,если угол АВС =120 градусов , ВМ =12 см

Я не имею понятия, как это решить.Но очень надеюсь,что вы мне поможете

Answer 1

1)ΔBKM и ΔBNM - прямоугольные

∠KBM=∠MBN=∠ABC/2

cos(∠ABC/2)=KB/BM, cos(∠ABC/2)=BN/BM ⇒ KB/BM=BN/BM, так как BM>0,

KB=BN

2)∠ABC=120° ⇒ ∠KBM=60°

BK=12 см

cos(∠KBM)=BK/BM ⇒ BK=cost(∠KBM)*BM

cos(60°)=1/2

BK=1/2*12=6 см