Question

сторона основи правильної трикутної призми дорівнює 4 см а їх бічне ребро 2^3см обчислити обєм призми

Answer 1

Ответ:

Об’єм призми дорівнює 24 см³

Объяснение:

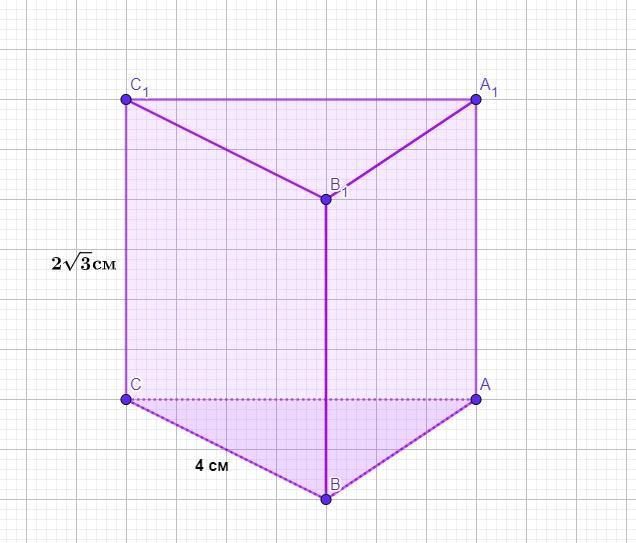
Сторона основи правильної трикутної призми дорівнює 4 см, а бічне ребро дорівнює 2√3 см. Знайти об’єм призми.

• Правильна трикутна призма – призма, в основі якої лежать два правильних трикутника (всі сторони яких дорівнюють, а кути між сторонами складають 60°), а всі бічні грані строго перпендикулярні цих основ.

Об’єм правильної призми обчислюється за формулою:

V=Sосн · h

де Sосн - площа основи, h - висота призми .

Так як у правильної призми всі бічні грані перпендикулярні основі, то бічне ребро і є висотою призми, за умовою h=2√3 см.

Треба знайти площу основи.

Так як ΔАВС - правильний, то АВ=ВС=АС=4 см

Площа правильного трикутника обчислюється за формулою:

$S=\dfrac{a^{2}\sqrt{3} }{4}$

a=4 см. Тому:

$S=\dfrac{4^{2}\cdot \sqrt{3} }{4} =4\sqrt{3}$ см²

Тоді об’єм правильної призми:

V = 4√3 · 2√3 = 8·3 = 24 см³

#SPJ5