Предмет: Алгебра,
автор: TequilaSunrise
помогите, пожалуйста, буду безмерно благодарна (:
Приложения:
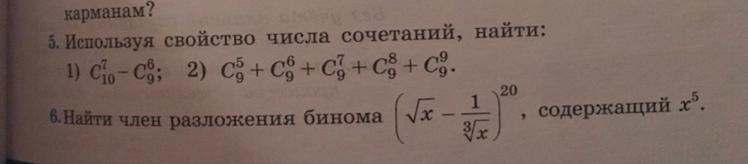
TequilaSunrise:
только 6 номер нужен
Ответы
Автор ответа:
1
Дан бином: (a+b)^20
a=√x=x^(1/2)
b=1/∛x= -x^(-1/3)
Найдем номер члена бинома:
a^(20-n) *b^n= x^ (1/2*(20-n)) * x^(-1/3* (n) ) *(-1)^n
1/2 *(20-n) -n/3=5 (нам нужна 5-я cтепень)
10 -n/2 -n/3=5
60-3n-2n=30
5n=30
n=6. ( (-1)^n=(-1)^6=1)
Коэффициент при разложении равен: C(n;20)=C(6;20)=20!/14!*6!=15*16*17*18*19*20/2*3*4*5*6=17*6*19*20=38760
Ответ: 38760*x^5
У нас n -член имеет вид С(k,20) *a^(20-k)*b^(k) . А член a^20 можно считать нулевым.
То что n=6 нет никаких сомнений
Я проверил на онлайн калькуляторе. Разложение в бином Ньютона
38760*x^5 правильный ответ
Можно в ручную даже взять пятую производную деленную на 5! в нуле. И получается это значение.
хорошо, спасибо) а что за 5 производная, деланная на 5 в нуле? о.О
Да это так. Если функция f(x) представляется степенным рядом. То если у ряда имеется целая степень a*x^k , то a=f(0)^^k/k! . Где ^^k -k-я производная функции в нуле.
Это и логично. Если для a*x^k , к раз взять производную получим: a*k! . А остальные члены,те что содержат x, обнулятся в нуле. f(0)^^k=a*k!
Этот простой примем как раз применяется для разложения любой функции в бесконечный степенной ряд (Ряд Тейлора).
Конечно не для любой функции, а для которой существует k-я производная в нуле
Похожие вопросы
Предмет: Українська мова,
автор: ktotoneponiatni
Предмет: Русский язык,
автор: dostaevaylvala
Предмет: Математика,
автор: Аноним
Предмет: Литература,
автор: ВладаВонхо
Предмет: Алгебра,
автор: elenaredkina