Здравствуйте. Возникла проблема с симметричными системами уравнений для трех неизвестных. Замены есть (какие выполняются), но не пойму как дальше после замены. Заранее спасибо!!!!
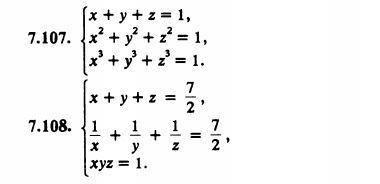
Ответы
1) x+y=1-z
x^2+y^2=(1-z^2)=(1-z)*(1+z)
x^3+y^3= (1-z^3)=(1-z)*( 1+z+z^2)
Положим что x≠-y , тогда возможно поделить второе уравнение на первое.
Делим второе уравнение на первое:
(x^2+y^2)/(x+y)= 1+z
cкладываем с:
(x^2+y^2)/(x+y) +x+y=(1-z)+(1+z)=2
(2x^2+2y^2+2xy)/(x+y)=2
x^2+xy+y^2=x+y
xy= (x+y) -(x^2+y^2)=(1-z)-(1-z^2)= z^2-z
x^3+y^3=(x+y)*(x^2-xy+y^2)=(1-z)*(1-z^2 -(z^2-z) )=(1-z)*(1+z-2z^2)=
=(1-z)*(1+z+z^2)
(1-z)*(1+z-2z^2 -1-z-z^2)=0
(1-z)*(-3z^2)=0
либо z=1 ; либо z=0
Если z=1, то x+y=0 ,что противоречит предположению, значит z=0.
x+y=1 (x^2+2xy+y^2=1)
x^2+y^2=1
2xy=0
либо x=0 , либо y=0.
Таким образом имеем решения:
(0;1;0) ;(1;0;0) ( в скобках (x;y;z) )
Либо, если x=-y → z=1 ,но тогда x^2+y^2=2x^2=0 →x=y=0 (0;0;1)
Таким образом решения- это все комбинации единички и двух нулей:
Ответ: (0;0;1) ; (0;1;0) ; (1;0;0)
2) Похожий принцип решения:
x+y=7/2 -z
1/x +1/y=7/2 -1/z=(x+y)/(xy)
xy=1/z
(7/2 -z)/(1/z) =7/2-1/z
(7/2-z)*z -7/2+1/z=0
тк z≠0
(7-2z)*z^2 -7z +2=0
7z^2-2z^3 -7z+2=0
7z*(z-1) -2*(z^3-1)=0
7z*(z-1) -2*(z-1)*(z^2+z+1)=0
(z-1)* (7z -2z^2-2z-2)=0
z1=1
-2z^2+5z-2=0
2z^2-5z+2=0
D=25 -16=9=3^2
z=(5+-3)/4
z2=2 ; z3=1/2
1) z1=1
x+y=5/2
xy=1
Cистема теоремы Виета имеет два симметричных решения,что можно найти подбором:
x1=2; y2=1/2
x2=1/2; y2=2
2) z2=2
Из симметрии задачи относительно x,y,z ,тк решений аналогично так же 2 симметричных имеем:
x3=1 ;y3=1/2
x4=1/2 ;y3=1
3) z3=1/2
x5=1 ; y5=2
x6=2 ; y6=1
Ответ: все перестановки чисел (1;1/2;2)