Предмет: Алгебра,
автор: dadagdgd
Хотя б одно, прошу. Даю много баллов
Приложения:
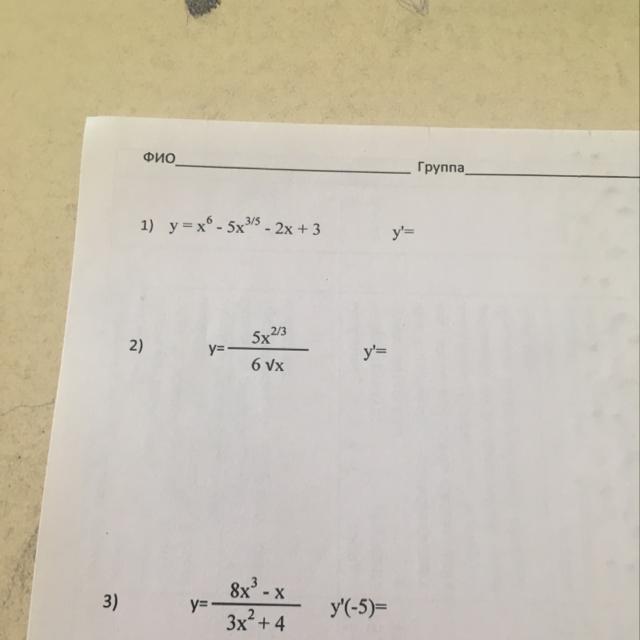
Ответы
Автор ответа:
1
Решение во вложении:
Приложения:

Автор ответа:
0
Похожие вопросы
Предмет: Математика,
автор: aferimeliyeva4
Предмет: Українська мова,
автор: vikaslobozhannb
Предмет: Русский язык,
автор: roibudavid538
Предмет: Математика,
автор: gaponova2004
Предмет: Алгебра,
автор: evelinakosimova