Предмет: Алгебра,
автор: Elay11
найдите точку максимума
Приложения:
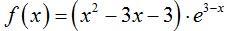
Ответы
Автор ответа:
0
________<0____0___>0______5____<0__________
f'=(2x-3)e^(3-x)-(x^2-3x-3)e^(3-x)=e^(3-x)(2x-3-x^2+3x+3)=
=e^(3-x)(5x-x^2)=0
5x-x^2=0
x=0 x=5
e^(3-x)>0
при переходе через точку 0, производная меняет знак с - на +
в точке имеется минимум f(0)=-3e^3
при переходе через точку 5, производная меняет знак с + на -
в точке имеется максимум f(5)=(25-15-3)e^(-2)=7*e^(-2)
Похожие вопросы
Предмет: Українська мова,
автор: digginout
Предмет: Геометрия,
автор: dashaeletckaya
Предмет: Информатика,
автор: ItzFANF
Предмет: Математика,
автор: Уля222
Предмет: Математика,
автор: VolkAngelina2005