Question

Помогите пожалуйста! sin6x*cos2x< sin5x*cos3x

Answer 1

Ответ:

Пошаговое объяснение:

по формуле sina*cosb=(1/2)[sin(a+b)+sin(a-b)]

sin6x*cos2x< sin5x*cos3x

(1/2)[sin(6x+2x)+sin(6x-2x)]<(1/2)[sin(5x+3x)+sin(5x-3x)]

sin(8x)+sin(4x)<sin(8x)+sin(2x)

sin(4x)<sin(2x)

sin(4x)-sin(2x)<0

2sin2xcos2x-sin2x<0

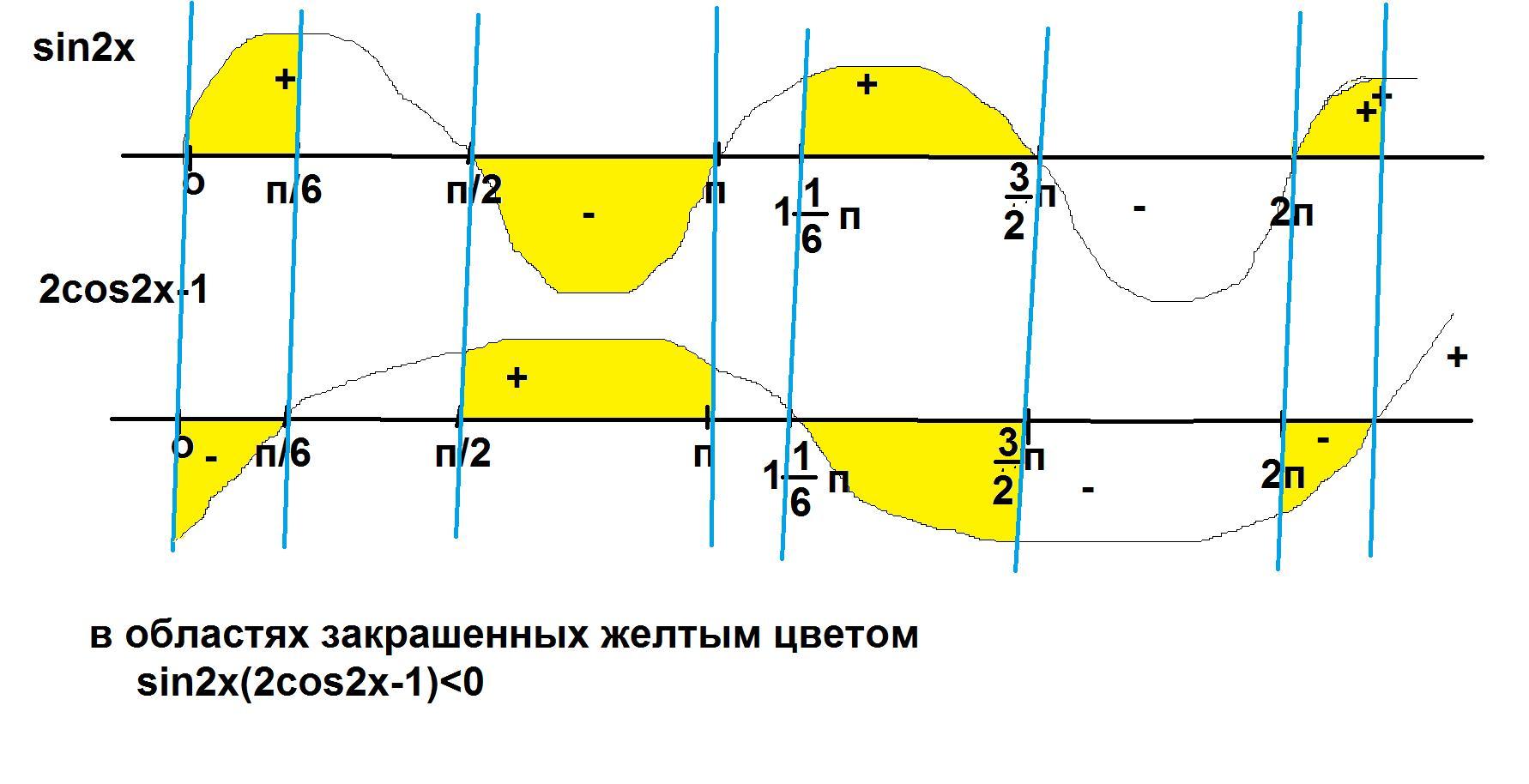
sin2x(2cos2x-1)<0

1) sin2x=0 ; 2x=пn, x=пn/2 , n∈Z

2) 2cos2x-1; cos2x=1/2; 2x=±arccos(1/2)+2пk=±п/3+2пk; x=±п/6+пk , k∈Z

рассмотрим решение неравенства методом интервалов на промежутке [0;2п] см. рис.

х∈(0;п/6)U(п/2;п)U((1 1/6)п; 3/2п)

с учетом периодичности

х∈(2пk;п/6+2пк)U(п/2+2пк;п+2пк)U((1 1/6)п+2пк; 3/2п+2пк), к∈Z